
【题目】某欢乐谷为回馈广大谷迷,在暑假期间推出学生个人门票优惠价,各票价如下:
票价种类 | (A)学生夜场票 | (B)学生日通票 | (C)节假日通票 |
单价(元) | 80 | 120 | 150 |
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生,其中购买的B种票数是A种票数的3倍还多7张,C种票y张.
(1)直接写出y与x之间的函数关系式;
(2)设购票总费用为w元,求w(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不低于20张,且每种票至少购买5张,则有几种购票方案?并指出哪种方案费用最少.
【答案】(1)y=93-4x;(2)w=-160x+14790;(3) 共有3种购票方案, 当A种票为22张,B种票73张,C种票为5张时费用最少,最少费用为11270元.
【解析】
试题(1)根据总票数为100得到x+3x+7+y=100,然后用x表示y即可;
(2)利用表中数据把三种票的费用加起来得到w=80x+120(3x+7)+150(93-4x),然后整理即可;
(3)根据题意得到 ,再解不等式组且确定不等式组的整数解为20、21、22,于是得到共有3种购票方案,然后根据一次函数的性质求w的最小值.
,再解不等式组且确定不等式组的整数解为20、21、22,于是得到共有3种购票方案,然后根据一次函数的性质求w的最小值.
试题解析:解:(1)x+3x+7+y=100,
所以y=93-4x;
(2)w=80x+120(3x+7)+150(93-4x)
=-160x+14790;
(3)依题意得 ,
,
解得20≤x≤22,
因为整数x为20、21、22,
所以共有3种购票方案(A、20,B、67,C、13;A、21,B、70,C、9;A、22,B、73,C、5);
而w=-160x+14790,
因为k=-160<0,
所以y随x的增大而减小,
所以当x=22时,y最小=22×(-160)+14790=11270,
即当A种票为22张,B种票73张,C种票为5张时费用最少,最少费用为11270元.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,已知直线![]() 经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB
经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB
(1)求直线![]() 的函数解析式
的函数解析式
(2)若直线![]() 也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标
也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
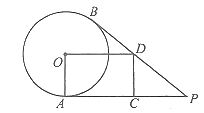
【题目】已知:如图,点![]() 是
是![]() 外一点,过点
外一点,过点![]() 分别作
分别作![]() 的切线
的切线![]() 、
、![]() ,切点为点
,切点为点![]() 、
、![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,
, ![]() 的半径为
的半径为![]() ,试证明四边形
,试证明四边形![]() 的周长等于
的周长等于![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月12日,Apple(苹果公司)发布了iPhone X。苹果公司某生产车间计划平均每天生产iPhone X手机200台,但是由于种种原因,实际每天生产量与计划生产量相比有出入.下表是某周的生产情况(超产记为正,减产即为负)

(1)根据记录的数据可知该车间星期三生产iPhone X手机 台?
(2)产量最多的一天比产量最少的一天多生产iPhone X手机 台?
(3)根据记录的数据可知该车间本周实际共生产iPhone X手机多少台?(请写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. ![]() 一定是一次函数
一定是一次函数
B. 有的实数在数轴上找不到对应的点
C. 长为![]() 的三条线段能组成直角三角形
的三条线段能组成直角三角形
D. 无论![]() 为何值,点
为何值,点![]() 总是在第二象限
总是在第二象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并完成任务:
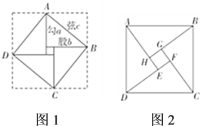
中国古代三国时期吴国的数学家赵爽最早对勾股定理作出理论证明.他创制了一幅“勾股圆方图”(如图l),用数形结合的方法,给出了勾股定理的详细证明.在这幅“勾股圆方图”中,以弦为边长得到的正方形![]() 是由
是由![]() 个全等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为
个全等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为![]() ;中间的小正方形边长为
;中间的小正方形边长为![]() ,面积为
,面积为![]() .于是便得到式子:
.于是便得到式子:![]() .赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.如图2,是“赵爽弦图”,其中
.赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.如图2,是“赵爽弦图”,其中![]() 、
、![]() 、
、![]() 和
和![]() 是四个全等的直角三角形,四边形
是四个全等的直角三角形,四边形![]() 和
和![]() 都是正方形,根据这个图形的面积关系,可以证明勾股定理.设
都是正方形,根据这个图形的面积关系,可以证明勾股定理.设![]() ,
,![]() ,
,![]() ,取
,取![]() ,
,![]() .
.
任务:
(1)填空:正方形![]() 的面积为______,四个直角三角形的面积和为______;
的面积为______,四个直角三角形的面积和为______;
(2)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com