Question

【题目】如图，是等边三角形，是边上的一点，以为边作等边三角形，使点在直线的同侧，连结.

(1)求证：.

(2)点在的延长线上，仍以为边作等边三角形，使得在直线的同侧，那么和还平行吗？画图证明你的判断.

Answer 1

【答案】（1）证明见详解，（2）同样有AE∥BC，作图证明见详解.

【解析】

(1) 先证明△ACE≌△BCD，继而可得∠EAC=∠B=60°=∠ACB，问题得证；

(2)画图并观察作图猜想AE∥BC，证明△ACE≌△BCD，继而推导出∠EAC+∠BCA=180°，即可得结论.

（1）∵△ABC和△DEC是等边三角形，

∴BC=AC，CD=CE，∠BCA=∠ECD，

∴∠BCA–∠DCA=∠ECD–∠DCA，

即∠BCD=∠ACE，

∵在△ACE和△BCD中AC=BC，∠ACE=∠BCD，CE=CD，

∴△ACE≌△BCD(SAS)，

∵∠B=60°，

∴∠EAC=∠B=60°=∠ACB，

∴AE∥BC.

（2）同样有AE∥BC，

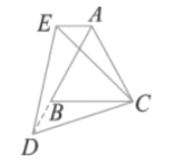
∵△ABC和△DEC是等边三角形，

∴BC=AC，CD=CE，∠BCA=∠ECD= ，

∵∠BCA–∠DCA=∠ECD–∠DCA，

∴∠BCD=∠ACE，

∵在△ACE和△BCD中AC=BC，∠ACE=∠BCD，CE=CD，

∴△ACE≌△BCD(SAS)，

∴∠EAC=∠DBC=120°，∠EAC+∠BCA=180°，

∴AE∥BC.