
【题目】已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
(1)观察图形并找出一对全等三角形:△_≌△_,请加以证明;
(2)在(1)中你所找出的一对全等三角形,其中一个三角形可由另一个三角形经过怎样的变换得到?
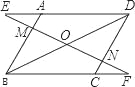
【答案】(1)△DOE≌△BOF;证明见解析;(2)绕点O旋转180°后得到或以点O为中心作对称变换得到.
【解析】
(1)本题要证明如△ODE≌△BOF,已知四边形ABCD是平行四边形,具备了同位角、内错角相等,又因为OD=OB,可根据AAS能判定△DOE≌△BOF;
(2)平行四边形是中心对称图形,这对全等三角形中的一个是以其中另一个三角形绕点O旋转180°后得到或以点O为中心作对称变换得到.
(1)△DOE≌△BOF;
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EDO=∠FBO,∠E=∠F.
又∵OD=OB,
∴△DOE≌△BOF(AAS).
(2)绕点O旋转180°后得到或以点O为中心作对称变换得到.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
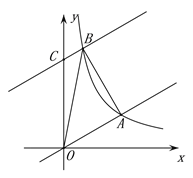
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x与反比例函数y=k/x在第一象限内的图象相交于点A(m,3).
x与反比例函数y=k/x在第一象限内的图象相交于点A(m,3).
(1)求该反比例函数的关系式;
(2)将直线y=![]() x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
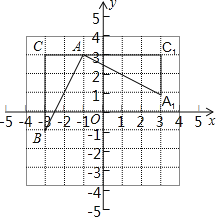
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
(3)设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有射线![]() 和点
和点![]() ,
,![]() ,请用尺规按下列要求作图:
,请用尺规按下列要求作图:
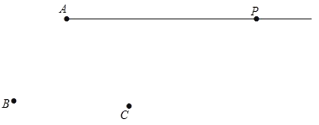
(1)连接![]() ,并在射线
,并在射线![]() 上截取
上截取![]() ;
;
(2)连接![]() 、
、![]() ,并延长
,并延长![]() 到
到![]() ,使
,使![]()
(3)在(2)的基础上,取![]() 中点
中点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
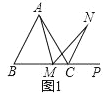
【题目】如图1所示,(1)在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点,若∠AMN=60°,求证:AM=MN.
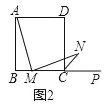
(2)若将(1)中“正三角形ABC”改为“正方形ABCD”,N是∠DCP的平分线上一点,若∠AMN=90°,则AM=MN是否成立?若成立,请证明;若不成立,说明理由.
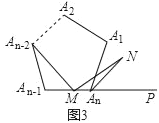
(3)若将(2)中的“正方形ABCD”改为“正n边形A1A2…An“,其它条件不变,请你猜想:当∠An﹣2MN=_____°时,结论An﹣2M=MN仍然成立.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
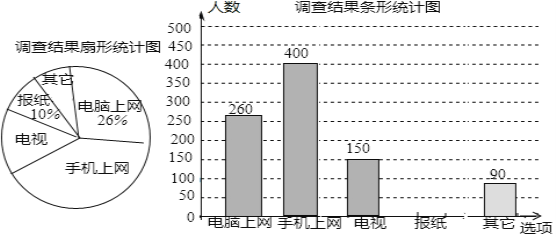
根据以上信息解答下列问题.
(1)这次抽样调查的样本容量是__________.
(2)通过“电视”了解新闻的人数占被调查人数的百分比为______;扇形统计图中,“手机上网”所对应的圆心角的度数是_________.
(3)请补全条形统计图;
(4)若该市约有950万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
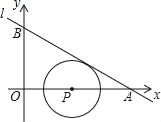
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com