
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,在⊙
,在⊙![]() 上一点
上一点![]() ,
,![]() .
.

(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)过![]() 作
作![]() 分别与
分别与![]() 、
、![]() 和⊙
和⊙![]() 交于点
交于点![]() 、
、![]() 、
、![]() ,若
,若![]() ,
,![]() .
.
①求⊙![]() 的半径长;
的半径长;
②直接写出![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】某医院医生为了研究该院某种疾病的诊断情况,需要调查来院就诊的病人的两个生理指标![]() ,
,![]() ,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
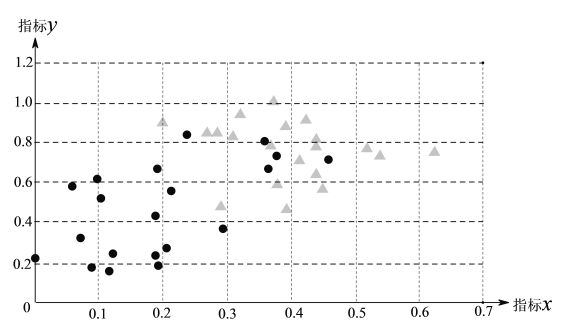
注“●”表示患者,“▲”表示非患者.
根据以上信息,回答下列问题:
(1)在这40名被调查者中,
①指标![]() 低于0.4的有 人;
低于0.4的有 人;
②将20名患者的指标![]() 的平均数记作
的平均数记作![]() ,方差记作
,方差记作![]() ,20名非患者的指标
,20名非患者的指标![]() 的平均数记作
的平均数记作![]() ,方差记作
,方差记作![]() ,则
,则![]()
![]() ,
,![]()
![]() (填“>”,“=”或“<”);
(填“>”,“=”或“<”);
(2)来该院就诊的500名未患这种疾病的人中,估计指标![]() 低于0.3的大约有 人;
低于0.3的大约有 人;
(3)若将“指标![]() 低于0.3,且指标
低于0.3,且指标![]() 低于0.8”作为判断是否患有这种疾病的依据,则发生漏判的概率多少.
低于0.8”作为判断是否患有这种疾病的依据,则发生漏判的概率多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半径为2的
,半径为2的![]() 从点
从点![]() 开始(如图①)沿直线
开始(如图①)沿直线![]() 向右滚动,滚动时始终与直线
向右滚动,滚动时始终与直线![]() 相切(切点为
相切(切点为![]() ),当
),当![]() 与
与![]() 只有一个公共点时滚动停止.作
只有一个公共点时滚动停止.作![]() 于点
于点![]() .
.
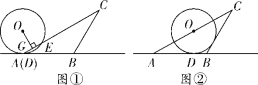
(1)图①中,![]() 在
在![]() 边上截得的弦长
边上截得的弦长![]() ______;
______;
(2)当圆心落在![]() 上时,如图②,判断
上时,如图②,判断![]() 与
与![]() 的位置关系,请说明理由;
的位置关系,请说明理由;
(3)在![]() 滚动过程中,线段
滚动过程中,线段![]() 的长度随之变化,设
的长度随之变化,设![]() ,
,![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并直接写出
之间的函数关系式,并直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2020B2020C2020D2020的边长是( )
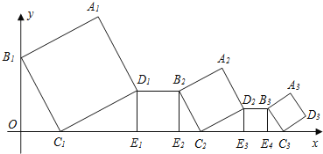
A.(![]() )2017B.(
)2017B.(![]() )2018C.(
)2018C.(![]() )2019D.(
)2019D.(![]() )2020
)2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与x轴、y轴相交于点B、C,经过点B、C的抛物线
分别与x轴、y轴相交于点B、C,经过点B、C的抛物线![]() 与x轴的另一个交点为A(-1,0).
与x轴的另一个交点为A(-1,0).
(1)求这个抛物线的表达式;
(2)已知点D在抛物线上,且横坐标为2,求出△BCD的面积;
(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于x轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,F为DA上一点,连接BF,E为BF中点,CD=6,sin∠ADB=![]() ,若△AEF的周长为18,则S△BOE=_____.
,若△AEF的周长为18,则S△BOE=_____.
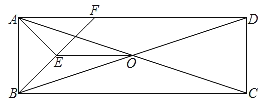
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题提出]
(1)如图![]() 均为等边三角形,点
均为等边三角形,点![]() 分别在边
分别在边![]() 上.将
上.将![]() 绕点
绕点![]() 沿顺时针方向旋转,连结
沿顺时针方向旋转,连结![]() .在图
.在图![]() 中证明
中证明![]() .
.
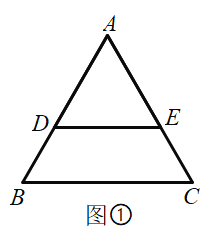

[学以致用]
(2)在![]() 的条件下,当点
的条件下,当点![]() 在同一条直线上时,
在同一条直线上时,![]() 的大小为 度.
的大小为 度.
[拓展延伸]
(3)在![]() 的条件下,连结
的条件下,连结![]() .若
.若![]() 直接写出
直接写出![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com