练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

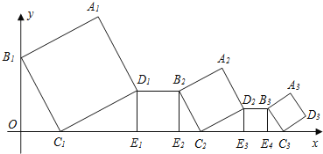
    【题目】一组正方形按如图所示的方式放置，其中顶点B1在y轴上，顶点C1，E1，E2，C2，E3，E4，C3……在x轴上，已知正方形A1B1C1D1的边长为1，∠B1C1O＝60°，B1C1∥B2C2∥B3C3……，则正方形A2020B2020C2020D2020的边长是（ ）

    A.()2017B.()2018C.()2019D.()2020

    【答案】C

    【解析】

    利用正方形的性质结合锐角三角形函数关系得出正方形的边长，进而得出变化规律即可得出答案．

    ∵正方形A1B1C1D1的边长为1，∠∠B1C1O=60°，B1C1∥B2C2∥B3C3，

    ∴D1E1=B2E2，D2E3=B3E4，∠D1C1E1=∠C2B2E2=∠C3B3E4=30°，

    ∴D1E1=C1D1sin30°=，

    则B2C2==，

    同理可得：B3C3=，

    故正方形AnBnCnDn的边长是：，

    则正方形A2020B2020C2020D2020的边长是：，

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，E是CD边上一点（CE>DE），AE，BD交于点F．

    （1）如图1，过点F作GH⊥AE，分别交边AD，BC于点G，H．

    求证：∠EAB=∠GHC；

    （2）AE的垂直平分线分别与AD，AE，BD交于点P，M，N，连接CN．

    ①依题意补全图形；

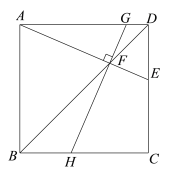
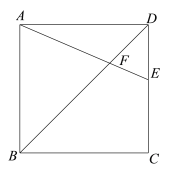
    图1 备用图

    ②用等式表示线段AE与CN之间的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某市有一块长为米，宽为米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，左右两边修两条宽为米的道路．（）．

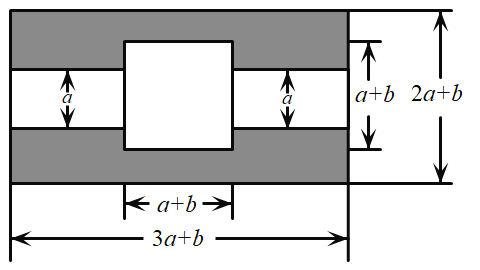
    （1）①试用含的代数式表示绿化的面积是多少平方米？

    ②假设阴影部分可以拼成一个矩形．请你求出所拼矩形相邻两边的长：如果要使所拼矩形面积最大，求与满足的关系式；

    （2）若，请求出绿化面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线与x轴交于A、B两点（A在B的左侧），与y轴的正半轴交于点C，顶点为D，对称轴与直线BC交于点E，且CE ：BE=1 ：2，连接BD，作CF//AB交抛物线对称轴于点H，交BD于点F．

    （1）写出A、B两点的坐标：A（ ， ），B（ ， ）

    （2）若四边形BEHF的面积为，求抛物线的函数表达式；

    （3）在（2）的条件下，抛物线对称轴上是否存在点M，使得∠CMF=∠CBF，若存在，请求出M点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，以为直径作⊙，在⊙上一点，．

    （1）求证：是⊙的切线；

    （2）过作分别与、和⊙交于点、、，若，．

    ①求⊙的半径长；

    ②直接写出的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某中学学生课余生活情况，对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计．现从该校随机抽取名学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名学生只能选择其中一项）．并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图．由图中提供的信息，解答下列问题：

    （1）求n的值；

    （2）若该校学生共有1200人，试估计该校喜爱看电视的学生人数；

    （3）若调查到喜爱体育活动的4名学生中有3名男生和1名女生，现从这4名学生中任意抽取2名学生，求恰好抽到2名男生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班，为了解学生对这四类兴趣班的喜爱情况，对学生进行了随机问卷调查(问卷调查表如图所示)，将调查结果整理后绘制了一幅不完整的统计表

    兴趣班

    频数

    频率

    合计

    请你根据统计表中提供的信息回答下列问题：

    （1）统计表中的_____， ；

    （2）根据调查结果，请你估计该市名小学生中最喜欢“绘画”兴趣班的人数；

    （3）王强和李昊选择参加兴趣班，若王强从三类兴趣班中随机选取一类，李吴从三类兴趣班中随机选取一类，请用画树状图或列表格的方法，求两人恰好选中同一类兴趣班的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．

    将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．大数学家海伦曾用轴对称的方法巧妙地解决了这个问题．

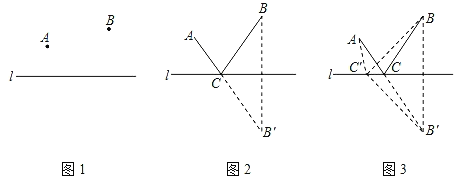
    如图2，作B关于直线l的对称点B′，连结AB′与直线l交于点C，点C就是所求的位置．

    证明：如图3，在直线l上另取任一点C′，连结AC′，BC′，B′C′，

    ∵直线l是点B，B′的对称轴，点C，C′在l上，

    ∴CB=CB′，C′B=C′B′，

    ∴AC+CB=AC+　 　=　 　．

    在△AC′B′中，

    ∵AB′＜AC′+C′B′

    ∴AC+CB＜AC′+C′B′即AC+CB最小．

    本问题实际上是利用轴对称变换的思想，把A，B在直线同侧的问题转化为在直线的两侧，从而可利用“两点之间线段最短”，即“三角形两边之和大于第三边”的问题加以解决（其中C在AB′与l的交点上，即A、C、B′三点共线）．本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型．

    1.简单应用

    （1）如图4，在等边△ABC中，AB=6，AD⊥BC，E是AC的中点，M是AD上的一点，求EM+MC的最小值

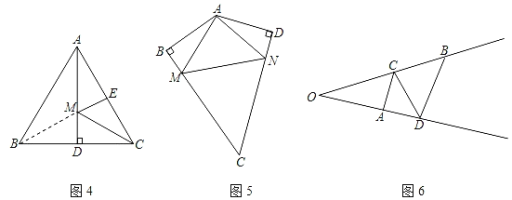
    借助上面的模型，由等边三角形的轴对称性可知，B与C关于直线AD对称，连结BM，EM+MC的最小值就是线段　 　的长度，则EM+MC的最小值是　 　；

    （2）如图5，在四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC，CD上分别找一点M、N当△AMN周长最小时，∠AMN+∠ANM=　 　°．

    2.拓展应用

    如图6，是一个港湾，港湾两岸有A、B两个码头，∠AOB=30°，OA=1千米，OB=2千米，现有一艘货船从码头A出发，根据计划，货船应先停靠OB岸C处装货，再停靠OA岸D处装货，最后到达码头B．怎样安排两岸的装货地点，使货船行驶的水路最短？请画出最短路线并求出最短路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是十堰市的三个旅游景点：丹江口的武当山、房县的野人洞、郧西县的五龙河的部分门票价格表．某单位在国庆长假前期给每人购买了一张门票，现将购买门票的情况绘制成如图所示的柱状统计图．

    景点

    标价（元/张）

    武当山

    200

    野人洞

    五龙河

    80

    请依据上表、图回答下列问题：

    （1）去武当山旅游的门票有________张，购买去野人洞旅游的门票占所有门票张数的____________．

    （2）若该单位采取随机抽取的方式把门票分配给员工，在看不到门票的前提下，每人抽取一张（所有门票形状、大小、颜色等完全相同且充分洗匀）．问员工小红抽取去武当山的门票的概率是___________．

    （3）若购买去五龙河的总款数占全部款数的．试求出每张野人洞门票的价格．

    查看答案和解析>>

    同步练习册答案