
【题目】早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.
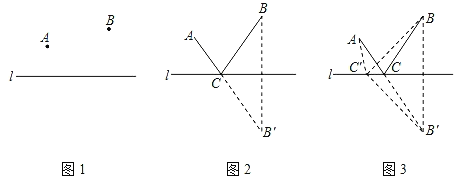
如图2,作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是所求的位置.
证明:如图3,在直线l上另取任一点C′,连结AC′,BC′,B′C′,
∵直线l是点B,B′的对称轴,点C,C′在l上,
∴CB=CB′,C′B=C′B′,
∴AC+CB=AC+ = .
在△AC′B′中,
∵AB′<AC′+C′B′
∴AC+CB<AC′+C′B′即AC+CB最小.
本问题实际上是利用轴对称变换的思想,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A、C、B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.
1.简单应用
(1)如图4,在等边△ABC中,AB=6,AD⊥BC,E是AC的中点,M是AD上的一点,求EM+MC的最小值
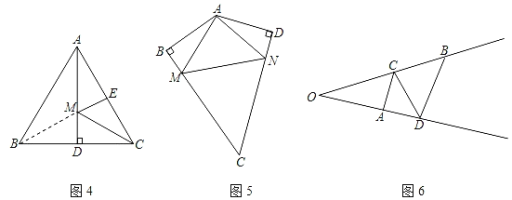
借助上面的模型,由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,EM+MC的最小值就是线段 的长度,则EM+MC的最小值是 ;
(2)如图5,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M、N当△AMN周长最小时,∠AMN+∠ANM= °.
2.拓展应用
如图6,是一个港湾,港湾两岸有A、B两个码头,∠AOB=30°,OA=1千米,OB=2千米,现有一艘货船从码头A出发,根据计划,货船应先停靠OB岸C处装货,再停靠OA岸D处装货,最后到达码头B.怎样安排两岸的装货地点,使货船行驶的水路最短?请画出最短路线并求出最短路程.
【答案】C′B;AB′;简单应用:(1)BE;3![]() ;(2)100;拓展应用:作图见解析,货船行驶的水路最短路程为
;(2)100;拓展应用:作图见解析,货船行驶的水路最短路程为![]() 千米
千米
【解析】
1.简单应用
(1)根据等边三角形的性质、勾股定理计算,得到答案;
(2)作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,根据等腰三角形的性质、三角形内角和定理计算;
2.拓展应用
分别作点A关于OB的对称点A′,点B关于OA的对称点B′,连接A′B′,交OB于C,交OA于D,根据轴对称的性质、勾股定理计算,得到答案.
解:AC+CB=AC+C′B=AB′,
故答案为:C′B;AB′;
1.简单应用
(1)由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,
EM+MC的最小值就是线段BE的长度,
BE=![]() ,
,
则EM+MC的最小值是![]() ,
,
故答案为:BE;![]() ;
;
(2)如图5,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,
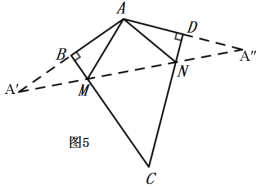
则A′A″即为△AMN的周长最小值,
∵∠DAB=130°,
∴∠A′+∠A″=50°,
∵∠A′=∠MAA′,∠NAD=∠A″,
且∠A′+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAD+∠A″=2(∠A′+∠A″)=2×50°=100°,
故答案为:100;
2.拓展应用
如图6,分别作点A关于OB的对称点A′,点B关于OA的对称点B′,连接A′B′,交OB于C,交OA于D,则C、D为两岸的装货地点,A′B′是货船行驶的水路最短路程,
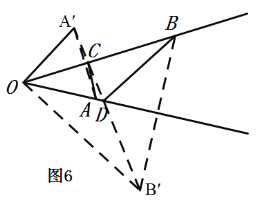
由轴对称的性质可知,OA′=OA=1,OB′=OB=2,∠BOA′=∠AOB=30°,∠AOB′=∠AOB=30°,
∴∠A′OB′=90°,
∴A′B′=![]() ,
,
答:货船行驶的水路最短路程为![]() 千米.
千米.


科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2020B2020C2020D2020的边长是( )
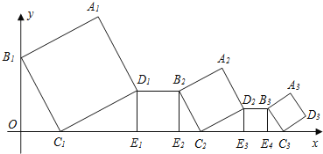
A.(![]() )2017B.(
)2017B.(![]() )2018C.(
)2018C.(![]() )2019D.(
)2019D.(![]() )2020
)2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
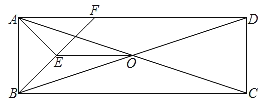
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,F为DA上一点,连接BF,E为BF中点,CD=6,sin∠ADB=![]() ,若△AEF的周长为18,则S△BOE=_____.
,若△AEF的周长为18,则S△BOE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
(1)求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数;
(2)将条形统计图补充完整;
(3)若规定:假期阅读3本及3本以上课外书者为完成假期作业,据此估计该校1500名学生中,完成假期作业的有多少名学生?

查看答案和解析>>
科目:初中数学 来源: 题型:
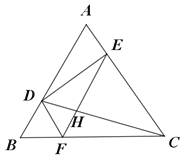
【题目】如图,等边三角形ABC的边长为6,点E为AC边上一点,AE=2,作DE⊥AC于点E交AB于点D,点F在BC边上且BF=BD.连接EF与CD交于点H,则DH的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解疫情期间学生每天网课学习情况,随机调查了部分学生,对学生每天网课时间x(单位:小时)进行分组整理,并绘制了如下图不完整的频数分布直方图和扇形统计图
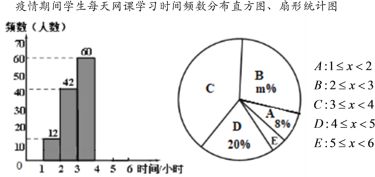
(1)请你补全频数分布直方图;
(2)求扇形统计图中m的值和C组对应的圆心角度数;
(3)请估计该校1000名学生中每天网课时间不小于3小时的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com