
【题目】某校想了解疫情期间学生每天网课学习情况,随机调查了部分学生,对学生每天网课时间x(单位:小时)进行分组整理,并绘制了如下图不完整的频数分布直方图和扇形统计图
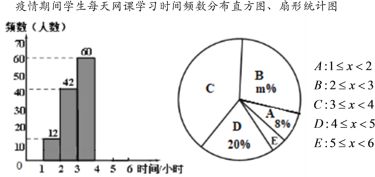
(1)请你补全频数分布直方图;
(2)求扇形统计图中m的值和C组对应的圆心角度数;
(3)请估计该校1000名学生中每天网课时间不小于3小时的人数.
【答案】(1)详见解析;(2)m=28;C组圆心角度数144°;(3)640人
【解析】
(1)根据A组频数为12,所占百分比为8%,求出数据总数,根据D组所占百分比为20%,可求出D组的频数,用数据总数减去其余各组频数得到E组频数,进而补全频数分布直方图;
(2)用B组频数除以数据总数,再乘以100,得到m的值;先求出“C”组所占百分比,再乘以360°即可求出对应的圆心角度数;
(3)用1000乘以每周每天网课时间不小于3小时的学生所占百分比即可.
(1)数据总数为:12÷8%=150,
D组频数为:150×20% =30,
E组频数为:150-12-42-60-30=6,
频数分布直方图补充如下:如右图所示
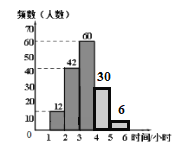
(2)m=42÷150×100=28;
“C”组对应的圆心角度数为:![]() ;
;
(3)![]() (人).
(人).
即估计该校1000名学生中每天网课时间不小于3小时的人数是640人


科目:初中数学 来源: 题型:
【题目】早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.
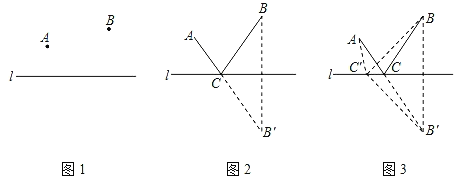
如图2,作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是所求的位置.
证明:如图3,在直线l上另取任一点C′,连结AC′,BC′,B′C′,
∵直线l是点B,B′的对称轴,点C,C′在l上,
∴CB=CB′,C′B=C′B′,
∴AC+CB=AC+ = .
在△AC′B′中,
∵AB′<AC′+C′B′
∴AC+CB<AC′+C′B′即AC+CB最小.
本问题实际上是利用轴对称变换的思想,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A、C、B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.
1.简单应用
(1)如图4,在等边△ABC中,AB=6,AD⊥BC,E是AC的中点,M是AD上的一点,求EM+MC的最小值
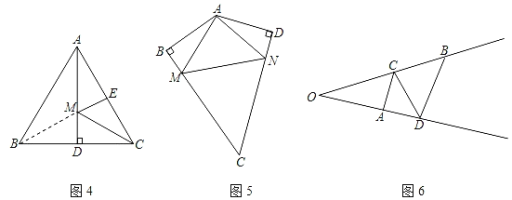
借助上面的模型,由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,EM+MC的最小值就是线段 的长度,则EM+MC的最小值是 ;
(2)如图5,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M、N当△AMN周长最小时,∠AMN+∠ANM= °.
2.拓展应用
如图6,是一个港湾,港湾两岸有A、B两个码头,∠AOB=30°,OA=1千米,OB=2千米,现有一艘货船从码头A出发,根据计划,货船应先停靠OB岸C处装货,再停靠OA岸D处装货,最后到达码头B.怎样安排两岸的装货地点,使货船行驶的水路最短?请画出最短路线并求出最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是十堰市的三个旅游景点:丹江口的武当山、房县的野人洞、郧西县的五龙河的部分门票价格表.某单位在国庆长假前期给每人购买了一张门票,现将购买门票的情况绘制成如图所示的柱状统计图.
景点 | 标价(元/张) |
武当山 | 200 |
野人洞 |
|
五龙河 | 80 |

请依据上表、图回答下列问题:
(1)去武当山旅游的门票有________张,购买去野人洞旅游的门票占所有门票张数的____________![]() .
.
(2)若该单位采取随机抽取的方式把门票分配给员工,在看不到门票的前提下,每人抽取一张(所有门票形状、大小、颜色等完全相同且充分洗匀).问员工小红抽取去武当山的门票的概率是___________.
(3)若购买去五龙河的总款数占全部款数的![]() .试求出每张野人洞门票的价格.
.试求出每张野人洞门票的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).
(1)求这个二次函数的表达式;
(2)过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
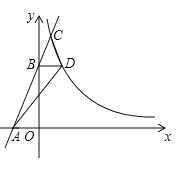
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]()
![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() 轴,交反比例函数
轴,交反比例函数![]()
![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的面积;
的面积;
(3)设![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,交反比例函数
轴,交反比例函数![]()
![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形,求点
为顶点的四边形为平行四边形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“孝敬”、“勤劳”是中华民族的传统美德,疫情期间同学们在家里经常帮助父母做一些力所能及的家务.学校随机调查了部分同学疫情期间在家做家务的总时间,设被调查的每位同学疫情期间在家做家务的总时间为![]() 小时,现将做家务的总时间分为五个类别:
小时,现将做家务的总时间分为五个类别:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .并将调查结果绘制成如下两幅不完整的统计图:
.并将调查结果绘制成如下两幅不完整的统计图:


请你根据统计图中提供的信息回答下列问题:
(1)本次共调查了多少名学生?
(2)通过计算补全条形统计图;
(3)若该校共有1000名学生,请你估计该校疫情期间在家做家务的总时间不低于20小时的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y![]() ,请根据已学知识探究该函数的图象和性质.
,请根据已学知识探究该函数的图象和性质.
(1)列表,写出表中a、b,c的值:a= ,b= ,c= ;
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0.5 | a | 2.5 | b | 2.5 | 1 | c | … |
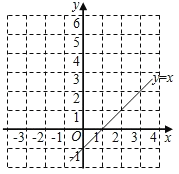
(2)描点,连线:在如图的平面直角坐标系中画出该函数的图象,并写出该函数的一条性质: ;
(3)已知函数y=x﹣1的图象如图所示,结合你所画的函数图象,直接写出不等式![]() x﹣1的解集: .
x﹣1的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=mx+k,与x轴,y轴分别交于点A,B,经过点A的抛物线y=ax2+bx﹣3a与x轴另一个交点为点D,AD=4,将点B向右平移5个单位长度,得到点C.
(1)求点C的坐标(用k表示);
(2)求抛物线的对称轴;
(3)若抛物线的对称轴在y轴右侧,连接BD,BD比BO长1,抛物线与线段BC恰有一个公共点,求直线y=mx+k的解析式和a的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com