
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]()
![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() 轴,交反比例函数
轴,交反比例函数![]()
![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
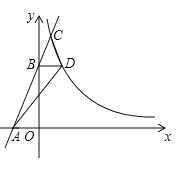
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的面积;
的面积;
(3)设![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,交反比例函数
轴,交反比例函数![]()
![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形,求点
为顶点的四边形为平行四边形,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1) 把点![]() 代入直线
代入直线![]() 得到b的值,再求解C的坐标。用待定系数法求解k的值即可得到答案;
得到b的值,再求解C的坐标。用待定系数法求解k的值即可得到答案;
(2) 根据一次函数的解析式得到B(0,4),把y=4代入![]() 得到
得到![]() ,根据三角形的面积公式即可得到结论;
,根据三角形的面积公式即可得到结论;
(3) 根据平行四边形的性质得到EF=AO=2,设点E(t,2t+4),①当点E位于点F的左侧时,得到点F(t+2,2t+4),②当点E位于点F的右侧时,得到点F(t-2,2t+4),解方程即可得到结论.
解:(1)把点![]() 代入直线
代入直线![]() 得到:
得到:
![]() ,
,
![]()
![]() 直线
直线![]()
当![]() ,则
,则![]() ,即点
,即点![]()
![]()
即反比例函数:![]()
(2)直线![]() 交
交![]() 轴于
轴于![]()
![]() 轴,
轴,
当![]() ,则
,则![]() ,即点
,即点![]()
![]() ;
;
(3)![]() 点
点![]() ,
,![]() ,
,![]() ,
,![]() 构成平行四边形
构成平行四边形
又![]()
![]()
设点![]()
①当点![]() 位于点
位于点![]() 左侧时
左侧时
![]() 则点
则点![]()
则![]()
![]()
![]()
![]()
![]()
②当点![]() 位于点
位于点![]() 右侧时,
右侧时,
![]() 则点
则点![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上所述,若以点A,O,E,F为顶点的四边形为平行四边形,点E的坐标为![]() 或
或![]() ;
;


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
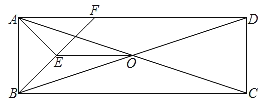
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,F为DA上一点,连接BF,E为BF中点,CD=6,sin∠ADB=![]() ,若△AEF的周长为18,则S△BOE=_____.
,若△AEF的周长为18,则S△BOE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题提出]
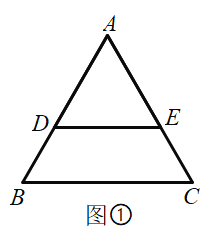
(1)如图![]() 均为等边三角形,点
均为等边三角形,点![]() 分别在边
分别在边![]() 上.将
上.将![]() 绕点
绕点![]() 沿顺时针方向旋转,连结
沿顺时针方向旋转,连结![]() .在图
.在图![]() 中证明
中证明![]() .
.

[学以致用]
(2)在![]() 的条件下,当点
的条件下,当点![]() 在同一条直线上时,
在同一条直线上时,![]() 的大小为 度.
的大小为 度.
[拓展延伸]
(3)在![]() 的条件下,连结
的条件下,连结![]() .若
.若![]() 直接写出
直接写出![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别是DA、BC延长线上的点,且∠ABE=∠CDF.
求证:(1)△ABE≌△CDF;
(2)四边形EBFD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
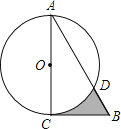
【题目】如图,在Rt△ABC中,∠A=30°,BC=4![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积等于________.(结果保留
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积等于________.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解疫情期间学生每天网课学习情况,随机调查了部分学生,对学生每天网课时间x(单位:小时)进行分组整理,并绘制了如下图不完整的频数分布直方图和扇形统计图
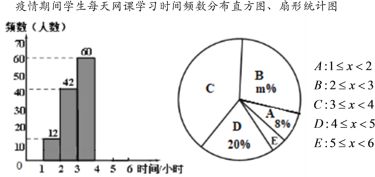
(1)请你补全频数分布直方图;
(2)求扇形统计图中m的值和C组对应的圆心角度数;
(3)请估计该校1000名学生中每天网课时间不小于3小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=15°.根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳,在上午10:00时,太阳光线与地面的夹角为65°,若要遮阳效果最佳AP的长约为( )
(参考数据:sin65°≈0.91,cos65°≈0.42,sin50°≈0.77,cos50°≈0.64)

A.1.2mB.1.3mC.1.5mD.2.0m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知气体的密度ρ与体积V是反比例函数关系,它的图象如图所示.
(1) 求密度ρ关于体积V的函数解析式;
(2) 当V=9m3时,求二氧化碳的密度ρ.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com