
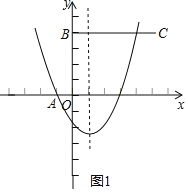
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y��mx��k����x�ᣬy��ֱ��ڵ�A��B��������A��������y��ax2��bx��3a��x����һ������Ϊ��D��AD��4������B����ƽ��5����λ���ȣ��õ���C��
��1�����C�����꣨��k��ʾ����
��2���������ߵĶԳ��
��3���������ߵĶԳ�����y���Ҳ࣬����BD��BD��BO��1�����������߶�BCǡ��һ�������㣬��ֱ��y��mx��k�Ľ���ʽ��a��ȡֵ��Χ��

���𰸡���1��C��5��k������2��x��1����x����1����3��y��4x��4��![]() ��
��![]() ��a����1��
��a����1��
��������
��1�������������ϵ���������������B�����꣬����ƽ�Ƶ����ʿ����C�����ꣻ
��2�������������ϵ���������������A�����꣬��һ����������ߵĶԳ��
��3�����ͼ�Σ��������������a��0����a��0���������ߵĶ������߶�BC�ϣ��������ۼ�����⣮
�⣺��1����y�ύ�㣺��x��0����ֱ��y��mx��k��y��k��
��B��0��k����
����B����ƽ��5����λ���ȣ��õ���C��
��C��5��k����
��2����y��0����������y��ax2��bx��3a�õ�x��![]()
��A��![]() ��0����D��
��0����D��![]() ��0��
��0��
��AD��4
��![]() ��4
��4
����ƽ���õ�
b2��4a(��3a)��16a2
��� b����2a��b��2a
�������ߵĶԳ���x��1����x����1��
��3���������ߵĶԳ�����y���Ҳ�
��x����![]() ��1 ��
��1 ��
��������y��ax2��2ax��3a
����A����1��0����D��3��0����
��BO��k����BD��k��1
��(k��1)2��k2��32
��k��4
��ֱ��y��mx��k����x�ᣬy��ֱ��ڵ�A��B
��ֱ��y��4x��4��
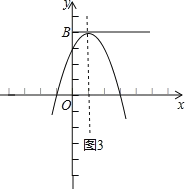
��a��0ʱ����ͼ1����x��0���������ߵ�y����3a��
�����������߶�BCǡ��һ�������㣬
����3a��4��a����![]() ��
��
��x��5���������ߵ�y��12a��
��12a��4��a��![]() ��
��
��a��![]() ��
��
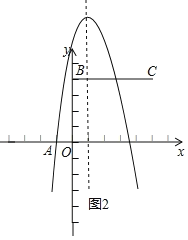
��a��0ʱ����ͼ2����x��0���������ߵ�y����3a��
�����������߶�BCǡ��һ�������㣬
����3a��4��a����![]() ��
��
��x��5���������ߵ�y��12a��
��12a��4��a��![]() ��
��
��a����![]() ��
��
���������ߵĶ������߶�BC��ʱ����Ϊ��1��4����
��ͼ3�����㣨1��4�����������ߵ�4��a��2a��3a��
���a����1��
����������ֱ�ߵĽ���ʽΪy��4x��4��a��ȡֵ��ΧΪa��![]() ��a����
��a����![]() ��a����1��
��a����1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���˽������ڼ�ѧ��ÿ������ѧϰ�������������˲���ѧ������ѧ��ÿ������ʱ��x����λ��Сʱ�����з���������������������ͼ��������Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ
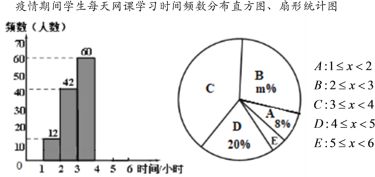
��1�����㲹ȫƵ���ֲ�ֱ��ͼ��
��2��������ͳ��ͼ��m��ֵ��C���Ӧ��Բ�ĽǶ�����
��3������Ƹ�У1000��ѧ����ÿ������ʱ�䲻С��3Сʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ڿ�չ�������й��������������Ȼ�У������������������������䷢��Ʒ����Ʒ�мס��ҡ����������ͣ���֪![]() �����ֽ�Ʒ�ļ۸���
�����ֽ�Ʒ�ļ۸���![]() �����ֽ�Ʒ�۸��
�����ֽ�Ʒ�۸��![]() ����
����![]() �����ֽ�Ʒ�ļ۸��
�����ֽ�Ʒ�ļ۸��![]() �����ֽ�Ʒ�ļ۸��
�����ֽ�Ʒ�ļ۸��![]() Ԫ����
Ԫ����![]() Ԫ�ֱ�ȥ����ס��ҡ������ֽ�Ʒ�����ͱ����ֽ�Ʒ�������������ֽ�Ʒ������
Ԫ�ֱ�ȥ����ס��ҡ������ֽ�Ʒ�����ͱ����ֽ�Ʒ�������������ֽ�Ʒ������![]() ����
����
��1����![]() ���ס��ҡ������ֽ�Ʒ�ļ۸�ֱ��Ƕ���Ԫ��
���ס��ҡ������ֽ�Ʒ�ļ۸�ֱ��Ƕ���Ԫ��
��2����У�ƻ�������ס��ҡ������ֽ�Ʒ��![]() �������й�����ֽ�Ʒ�������DZ��ֽ�Ʒ��
�������й�����ֽ�Ʒ�������DZ��ֽ�Ʒ��![]() �����Ҽ��ֽ�Ʒ�������������ҡ������ֽ�Ʒ������֮�ͣ����У��ɹ���ƻ����Ҫ���Ѷ���Ԫ��
�����Ҽ��ֽ�Ʒ�������������ҡ������ֽ�Ʒ������֮�ͣ����У��ɹ���ƻ����Ҫ���Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ͼ��ʾ��������̨����O-M-N�������ߣ����ӵ�O�������ؼ�ͷ��ʾ�ķ�����M���ߵ���N������ʱ70������һ̨�����ѡ����һ���̶���λ�ü�¼��С������·���̣���С����·��ʱ��Ϊt����λ������������������ľ���Ϊy����λ����������ʾy��t�ĺ�����ϵ��ͼ�������ͼ����������̶�λ�ÿ�����ͼ���е�
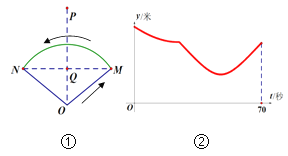
A����Q B����P C����M D����N
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ܱ���������һ�������Ķ�����̼�������������V(��λ��m3)�仯ʱ��������ܶ�������λ��kg/m3)��֮�仯����֪������ܶ��������V�Ƿ�����������ϵ������ͼ����ͼ��ʾ��
(1) ���ܶ����������V�ĺ�������ʽ;
(2) ��V=9m3ʱ���������̼���ܶ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ŵ�С���ʵؾ���ͬ�Ŀ�Ƭ�ϸ�дһ�����֣��ֱ�Ϊ5��6��8��8���ֽ����ſ�Ƭ����һֻ�����ĺ�����.
��1�������ĸ����ֵ�������
��2�����׳���һ��д��������6���Ŀ�Ƭ.
��ʣ�����ſ�Ƭ���������ֵ���λ����ԭ�����ſ�Ƭ���ĸ����ֵ���λ���Ƿ���ͬ����˵�����ɣ�
�ڽ��Ⱥ�������ʣ������ſ�Ƭ�������ȡһ�ſ�Ƭ���������ֺ�Żأ����Ⱥ��������ȡһ�ţ���������.������������ͬ���ֿ�Ƭ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С����ѧ�õ����г����ͺ���24Ӣ�������ֵ�ֱ��Ϊ24Ӣ����Լ60���ף���Ϊ�˷�ֹ���������ﳵʱ����ˮ�������ϣ����������г����ֵ���Ӱ��������װ�ϵ�ˮ����Ƥ��������Ӱ���ֱַ�����C��DΪԲ�ĵ��������Σ��������ı���ABCD�С�DAB=125������ABC=115������ôԤ����Ҫ����Ƥ���Լ�ǣ� ��

A.300��cm2B.600��cm2C.900��cm2 D.1200��cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽����м�ͥ�¾��õ���������йز���������������1000����ͥ���¾��õ������������������������£�
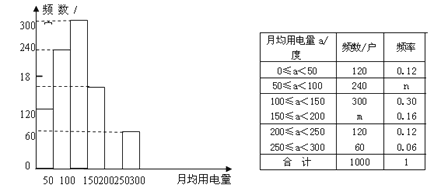
��1��Ƶ���ֲ����е�m=����������n=����������
��2����ȫƵ���ֲ�ֱ��ͼ��
��3���������1000����ͥ�¾��õ���������������һ����Χ��
��4�����¾��õ���С��150�ȵļ�ͥ��ռ�������ͥ�����İٷֱȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���ѧ���忼�ɼ�����ȫУ300�����꼶ѧ������һ��������ѵ����Ϊ�˽�ѧ��ѵ��Ч����ѧУ�������ھ��꼶��ѧ�ڿ�ѧ����ѧ��ĩ�ֱ�Ծ��꼶ѧ������һ�����������ԣ�ѧ���ɼ���Ϊ����������20�֣�����18��Ϊ���㣮�������ȡ��ͬһ����ѧ�������γɼ����������������ͷ��������ɼ��÷���x��ʾ�����ֳ����飺A��x��13��B.13��x��15��C.15��x��17��D.17��x��19��E.19��x��20��
��ѧ����ȡѧ���ijɼ���D���е������ǣ�17��17��17��17��17��18��18��
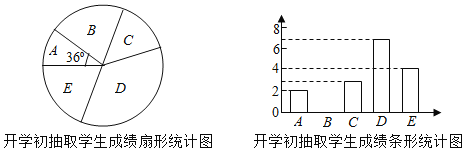
ѧ��ĩ��ȡѧ���ɼ�ͳ�Ʊ�
ѧ���ɼ� | A�� | B�� | C�� | D�� | E�� |
���� | 0 | 1 | 4 | 5 | a |
�������ݣ�
ƽ���� | ��λ�� | ���� | |
��ѧ����ȡѧ���ɼ� | 16 | b | 17 |
ѧ��ĩ��ȡѧ���ɼ� | 18 | 18.5 | 19 |
����������Ϣ������������⣺
��1��ֱ��д��ͼ����a��b��ֵ������ȫ����ͳ��ͼ��
��2�������У���꼶ѧ�����μ������β��ԣ����Ƹ�Уѧ��ĩ�ɼ������ѧ�������ȿ�ѧ���ɼ������ѧ�����������˶��٣�
��3��С��ѧ�����Գɼ�16�֣�ѧ��ĩ���Գɼ�19�֣����ݳ���������ݣ���ѡ��һ�����ʵ�ͳ��������С���ѵ��Ч����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com