
【题目】如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).
(1)求这个二次函数的表达式;
(2)过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.

【答案】(1)y=﹣2x2+4x+1;(2)S△APC最大值为![]() ,此时P(
,此时P(![]() ,
,![]() )
)
【解析】
(1)根据题意设这个二次函数的表达式为y=a(x﹣1)2+3,将A(0,1)代入解方程即可求解;
(2)直线AB与x轴交于点D,直线AC与x轴交于点E,先求得直线AC的解析式,即可求得抛物线和直线AC的交点C的坐标,过P作PQ∥y轴交AC于Q,根据抛物线解析式和直线AC的解析式设出P,Q点坐标,横坐标用t表示,即可表示出PQ,根据S△APC=![]() PQ|xC﹣xA|,得出关于t的二次函数,化为顶点式,即可得到当t为何值时,S△APC有最大值.
PQ|xC﹣xA|,得出关于t的二次函数,化为顶点式,即可得到当t为何值时,S△APC有最大值.
(1)∵抛物线的顶点为B(1,3)
∴设这个二次函数的表达式为y=a(x﹣1)2+3
∵二次函数的图象经过点A(0,1)
∴a(0﹣1)2+3=1
解得:a=﹣2
∴二次函数的表达式为y=-2(x﹣1)2+3,即y=﹣2x2+4x+1
故答案为:y=﹣2x2+4x+1
(2)直线AB与x轴交于点D,直线AC与x轴交于点E,如图所示
∵A(0,1),B(1,3)
设直线AB的解析式为y=kx+b
∴![]()
∴y=2x+1
令2x+1=0
解得x=![]()
∴OD=![]()
![]() ,
,![]()
∵AC⊥AB
∴∠DAE=90°
∴![]()
∴![]()
解得OE=2
∴E(2,0)
设直线AC的解析式为y=mx+n
∵直线AC经过A点,E点
∴![]()
∴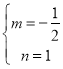
∴直线AC的解析式为y=![]() x+1
x+1
令![]() x+1=﹣2x2+4x+1
x+1=﹣2x2+4x+1
解得:![]() 或
或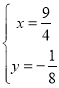
∴C(![]() ,
,![]() )
)
过P作PQ∥y轴交AC于Q
设P(t,﹣2t2+4t+1),则Q(t,![]() t+1)
t+1)
∴PQ=(﹣2t2+4t+1)﹣(![]() t+1)=﹣2t2+
t+1)=﹣2t2+![]() t
t
∴S△APC=![]() PQ|xC﹣xA|=
PQ|xC﹣xA|=![]() (﹣2t2+
(﹣2t2+![]() t)(
t)(![]() ﹣0)=﹣
﹣0)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]()
∴当t=![]() 时,S△APC有最大值
时,S△APC有最大值![]() ,此时,P(
,此时,P(![]() ,
,![]() )
)

故答案为:S△APC最大值为![]() ,此时P(
,此时P(![]() ,
,![]() )
)


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系,相似比为1:3,∠ACB=∠CED=90°,A、C、E是x轴正半轴上的点,B、D是第一象限的点,BC=2,则点D的坐标是( )
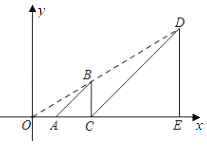
A.(9,6)B.(8,6)C.(6,9)D.(6,8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别是DA、BC延长线上的点,且∠ABE=∠CDF.
求证:(1)△ABE≌△CDF;
(2)四边形EBFD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次防灾抗灾过程中,为了保障某市的抗灾物资供应,现有一批救灾物资由![]() ,
,![]() 两种型号的货车运输至该市.已知
两种型号的货车运输至该市.已知![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车共可满载救灾物资
型货车共可满载救灾物资![]() 吨,
吨,![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车共可满载救灾物资
型货车共可满载救灾物资![]() 吨.
吨.
(1)求![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车分别能满载多少吨;
型货车分别能满载多少吨;
(2)已知这批救灾物资共![]() 吨,计划同时调用
吨,计划同时调用![]() ,
,![]() 两种型号的货车共
两种型号的货车共![]() 辆,并要求一次性将全部物资运送到该市,试求调用
辆,并要求一次性将全部物资运送到该市,试求调用![]() ,
,![]() 两种型号的货车的方案.
两种型号的货车的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解疫情期间学生每天网课学习情况,随机调查了部分学生,对学生每天网课时间x(单位:小时)进行分组整理,并绘制了如下图不完整的频数分布直方图和扇形统计图
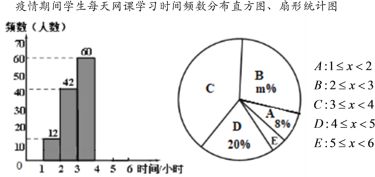
(1)请你补全频数分布直方图;
(2)求扇形统计图中m的值和C组对应的圆心角度数;
(3)请估计该校1000名学生中每天网课时间不小于3小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解一批口罩的质量适合采用的调查方式是全面调查
B.“任意画一个三角形,其内角和为180°”是随机事件
C.袋中有形状、大小、质地完全一样的6个红球和1个白球,从中随机抽出一个球,一定是红球
D.甲、乙两人进行射击练习,在相同条件下各射击10次,他们成绩的平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小阳在如图所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图②,则这个固定位置可能是图①中的
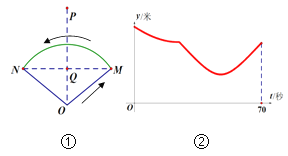
A.点Q B.点P C.点M D.点N
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com