
【题目】在某次防灾抗灾过程中,为了保障某市的抗灾物资供应,现有一批救灾物资由![]() ,
,![]() 两种型号的货车运输至该市.已知
两种型号的货车运输至该市.已知![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车共可满载救灾物资
型货车共可满载救灾物资![]() 吨,
吨,![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车共可满载救灾物资
型货车共可满载救灾物资![]() 吨.
吨.
(1)求![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车分别能满载多少吨;
型货车分别能满载多少吨;
(2)已知这批救灾物资共![]() 吨,计划同时调用
吨,计划同时调用![]() ,
,![]() 两种型号的货车共
两种型号的货车共![]() 辆,并要求一次性将全部物资运送到该市,试求调用
辆,并要求一次性将全部物资运送到该市,试求调用![]() ,
,![]() 两种型号的货车的方案.
两种型号的货车的方案.
科目:初中数学 来源: 题型:
【题目】某水果商将一种高档水果放在商场销售,该种水果成本价为10元![]() ,售价为40元
,售价为40元![]() ,每天可销售20
,每天可销售20![]() .调查发现,销售单价每下降1元,每天的销售量将增加5
.调查发现,销售单价每下降1元,每天的销售量将增加5![]() .
.
(1)直接写出每天的销售量ykg与降价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)降价多少元时,每天的销售额![]() 元最大,最大是多少元?(销售额=售价×数量)
元最大,最大是多少元?(销售额=售价×数量)
(3)每销售1![]() 水果,需向商场缴纳柜台费
水果,需向商场缴纳柜台费![]() 元(
元(![]() ),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润
),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润![]() 元随销售天数
元随销售天数![]() (
(![]() 为正整数)的增大而增大,试确定
为正整数)的增大而增大,试确定![]() 的取值范围.(利润=销售额-成本-柜台费)
的取值范围.(利润=销售额-成本-柜台费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数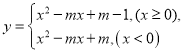 将此函数的图象记为
将此函数的图象记为![]() .
.
(1)当![]() 时,
时,
![]() 直接写出此函数的函数表达式.
直接写出此函数的函数表达式.
![]() 点
点![]() 在图象
在图象![]() 上,求点
上,求点![]() 的坐标.
的坐标.
![]() 点
点![]() 在图象
在图象![]() 上,求
上,求![]() 的值.
的值.
(2)设图象![]() 最低点的纵坐标为
最低点的纵坐标为![]() .当
.当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
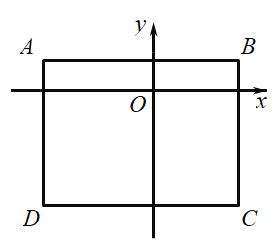
(3)矩形![]() 的顶点坐标分别为
的顶点坐标分别为![]() 若函数
若函数 在
在![]() 范围内的图象与矩形
范围内的图象与矩形![]() 的边有且只有一个公共点,直接写出此时
的边有且只有一个公共点,直接写出此时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=2,∠ABC=30°,AD为BC边上的高,E、F分别为AB、AC边上的点,将△ABC分别沿DE、DF折叠,使点B落在DA的延长线上点M处,点C落在点N处,连接MN,若MN∥AC,则AF的长是_____.
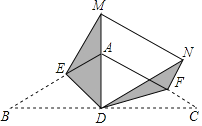
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).
(1)求这个二次函数的表达式;
(2)过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]()
![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,交
,交![]() 轴于点
轴于点![]() ,且抛物线的对称轴经过点
,且抛物线的对称轴经过点![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,点
,点![]() 是该抛物线上一点,连接
是该抛物线上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直线![]() 及抛物线的函数表达式;
及抛物线的函数表达式;
(2)试问:![]() 轴上是否存在某一点
轴上是否存在某一点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() 为顶点的
为顶点的![]() 与
与![]() 相似?若相似,请求出此时点
相似?若相似,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() ,
,![]() 重合),过
重合),过![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,则
,则![]() 在直线
在直线![]() 上所截得的线段长度的最大值等于_______.(直接写出答案)
上所截得的线段长度的最大值等于_______.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图
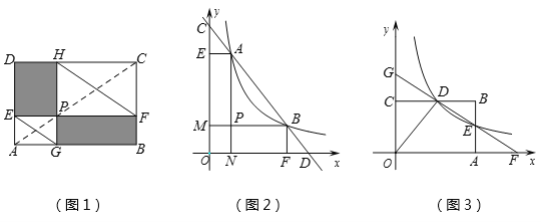
(1)方法体验:
如图1,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H,容易证明四边形PEDH和四边形PFBG是面积相等的矩形,分别连结EG,FH.
①根据矩形PEDH和矩形PFBG面积相等的关系,那么PE·PH= .
②求证:EG∥FH.
(2)方法迁移:
如图2,已知直线 ![]() 分别与x轴,y轴交于D,C两点,与双曲线
分别与x轴,y轴交于D,C两点,与双曲线 ![]() 交于A,B两点. 求证:AC=BD.
交于A,B两点. 求证:AC=BD.
(3)知识应用:
如图3,反比例函数 ![]() (x>0)的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴,y轴分别交于点F,G .若矩形ABCO的面积为10,△ODG与△ODF的面积比为3:5,则k=________.
(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴,y轴分别交于点F,G .若矩形ABCO的面积为10,△ODG与△ODF的面积比为3:5,则k=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com