
【题目】如图
(1)方法体验:
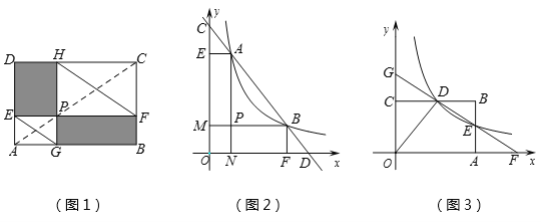
如图1,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H,容易证明四边形PEDH和四边形PFBG是面积相等的矩形,分别连结EG,FH.
①根据矩形PEDH和矩形PFBG面积相等的关系,那么PE·PH= .
②求证:EG∥FH.
(2)方法迁移:
如图2,已知直线 ![]() 分别与x轴,y轴交于D,C两点,与双曲线
分别与x轴,y轴交于D,C两点,与双曲线 ![]() 交于A,B两点. 求证:AC=BD.
交于A,B两点. 求证:AC=BD.
(3)知识应用:
如图3,反比例函数 ![]() (x>0)的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴,y轴分别交于点F,G .若矩形ABCO的面积为10,△ODG与△ODF的面积比为3:5,则k=________.
(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴,y轴分别交于点F,G .若矩形ABCO的面积为10,△ODG与△ODF的面积比为3:5,则k=________.
【答案】(1)①PGPF;②证明见解析;(2)证明见解析;(3)6
【解析】
(1)①矩形PEDH的面积为:PH·PE;矩形PFBG的面积为:PF·PG,由此可得结果;
②PH·PE= PF·PG,可得![]() ,可得△EPG∽△FPH,得∠PEG=∠PFH,证得结果;
,可得△EPG∽△FPH,得∠PEG=∠PFH,证得结果;
(2)由k的几何意义,得四边形MPAE的面积=四边形NPBF的面积,可证△APB∽△NPM,MN![]() AB,得四边形ACMN与四边形DBMN均是平行四边形,证得结果;
AB,得四边形ACMN与四边形DBMN均是平行四边形,证得结果;
(3)作DH![]() OA,由面积比得到GD:DF=3:5,由(2)的GD=EF,进一步得到GD,DE,EF的比例关系,设出D(
OA,由面积比得到GD:DF=3:5,由(2)的GD=EF,进一步得到GD,DE,EF的比例关系,设出D(![]() ),用DH
),用DH![]() OG
OG![]() AB,表示出AO,AB的长度,利用矩形面积求出k.
AB,表示出AO,AB的长度,利用矩形面积求出k.
(1)①由图知:矩形PEDH的面积为:PH·PE;矩形PFBG的面积为:PF·PG,
故答案为:PGPF;
②解:∵PEPH= PGPF
∴ ![]() 又∵∠EPG=∠HPF=90°
又∵∠EPG=∠HPF=90°
∴△EPG∽△FPH
∴∠PEG=∠PFH
∴EG∥FH
(方法二,如图,记FH,EG与AC交与M,N,
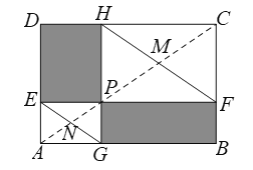
则PM=MH,PN=NG,
∴∠MPH=∠MHP, ∠NPG=∠NGP,
又∵∠NPG=∠MPH,
∴∠MHP=∠NGP
∴EG∥FH
(2)解:先利用四边形OEAN的面积=四边形OFBM的面积=k的绝对值;
∴四边形MPAE的面积=四边形NPBF的面积
∴ ![]() 即
即 ![]()
又∵∠APB=∠NPM=90°
∴△APB∽△NPM
∴∠ABP=∠PMN
∴MN∥AB
易得四边形ACMN与四边形DBMN均是平行四边形
∴AC=MN=BD
(3)作DH![]() OA于H
OA于H

∵△ODG与△ODF的面积比为3:5
∴![]()
设![]() ,则
,则![]()
由(2)知:![]()
设D(![]() ),即
),即![]()
由![]() ,得
,得![]() ,即
,即![]()
又![]() ,得
,得![]()
∴![]()
∴![]()
∴![]() ,解得
,解得![]() .
.


科目:初中数学 来源: 题型:
【题目】在某次防灾抗灾过程中,为了保障某市的抗灾物资供应,现有一批救灾物资由![]() ,
,![]() 两种型号的货车运输至该市.已知
两种型号的货车运输至该市.已知![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车共可满载救灾物资
型货车共可满载救灾物资![]() 吨,
吨,![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车共可满载救灾物资
型货车共可满载救灾物资![]() 吨.
吨.
(1)求![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车分别能满载多少吨;
型货车分别能满载多少吨;
(2)已知这批救灾物资共![]() 吨,计划同时调用
吨,计划同时调用![]() ,
,![]() 两种型号的货车共
两种型号的货车共![]() 辆,并要求一次性将全部物资运送到该市,试求调用
辆,并要求一次性将全部物资运送到该市,试求调用![]() ,
,![]() 两种型号的货车的方案.
两种型号的货车的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李辉到服装专卖店去做社会调查,了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法,并获得了如下信息:
营业员 | 嘉琪 | 嘉善 |
月销售件数/件 | 400 | 300 |
月总收入/元 | 7800 | 6600 |
假设月销售件数为x件,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员嘉善某月总收入不低于4200元,那么嘉善当月至少要卖多少件衣服?
查看答案和解析>>
科目:初中数学 来源: 题型:
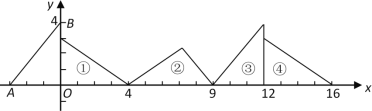
【题目】如图,在直角坐标系中,已知点![]() ,
,![]() ,对△
,对△![]() 连续作旋转变换,依次得到三角形①、②、③、④…,则连续作旋转变第10的三角形的直角顶点的坐标为____.连续作旋转变第2011的第号三角形的直角顶点的坐标为____.
连续作旋转变换,依次得到三角形①、②、③、④…,则连续作旋转变第10的三角形的直角顶点的坐标为____.连续作旋转变第2011的第号三角形的直角顶点的坐标为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小阳在如图所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图②,则这个固定位置可能是图①中的
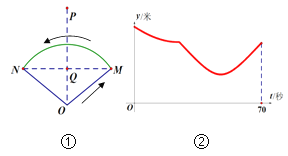
A.点Q B.点P C.点M D.点N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年受新冠病毒疫情的影响,王大伯家的两种水果“沃柑”和“夏橙”存在销售困难,这一情况被住村干部得知后,决定帮助王大伯提供线上(网上销售)和线下(批发给店铺)两种形式销售.通过一个星期的销售,其中通过线上销售1600斤,且通过线上销售的斤数比线下销售的斤数多60%.
(1)求王大伯的一星期线上线下销售“沃柑”和“夏橙”一共多少斤?
(2)如果销售的这些水果中“沃柑”比“夏橙”的2倍少700斤,而通过线上销售的“夏橙”的斤数不小于线下销售“夏橙”的2倍,则通过线下销售的“沃柑”至少多少斤?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张大小、质地均相同的卡片上各写一个数字,分别为5,6,8,8,现将四张卡片放入一只不透明的盒子中.
(1)求这四个数字的众数;
(2)若甲抽走一张写有数字“6”的卡片.
①剩下三张卡片的三个数字的中位数与原来四张卡片的四个数字的中位数是否相同?并说明理由;
②搅匀后乙准备从剩余的三张卡片中随机抽取一张卡片,记下数字后放回,搅匀后再任意抽取一张,记下数字.求两次摸到不同数字卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
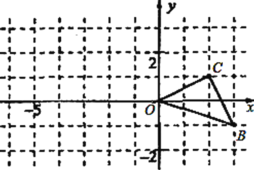
【题目】如图,方格纸中的每个小正方格都是边长为1的正方形,我们把以格点间连接为边的三角形称为“格点三角形”,图中的![]() 就是格点三角形,在建立平面直角坐标系后,O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)
就是格点三角形,在建立平面直角坐标系后,O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)
(1)以O点为位似中心在![]() 轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),在该坐标系中画出图形;
轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),在该坐标系中画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为加快5G网络建设,某通信公司在一个坡度i=1:2.4的山坡AB上建了一座信号塔CD,信号塔底端C到山脚A的距离AC=13米,在距山脚A水平距离18米的E处,有一高度为10米的建筑物EF,在建筑物顶端F处测得信号塔顶端D的仰角为37°(信号塔及山坡的剖面和建筑物的剖面在同一平面上),则信号塔CD的高度约是( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
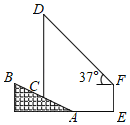
A.22.5米B.27.5米C.32.5米D.45.0米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com