
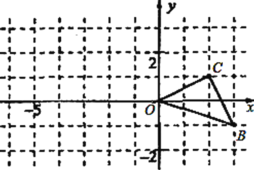
【题目】如图,方格纸中的每个小正方格都是边长为1的正方形,我们把以格点间连接为边的三角形称为“格点三角形”,图中的![]() 就是格点三角形,在建立平面直角坐标系后,O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)
就是格点三角形,在建立平面直角坐标系后,O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)
(1)以O点为位似中心在![]() 轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),在该坐标系中画出图形;
轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),在该坐标系中画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图
(1)方法体验:
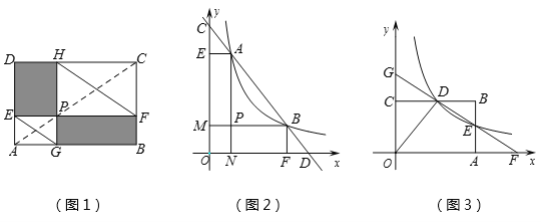
如图1,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H,容易证明四边形PEDH和四边形PFBG是面积相等的矩形,分别连结EG,FH.
①根据矩形PEDH和矩形PFBG面积相等的关系,那么PE·PH= .
②求证:EG∥FH.
(2)方法迁移:
如图2,已知直线 ![]() 分别与x轴,y轴交于D,C两点,与双曲线
分别与x轴,y轴交于D,C两点,与双曲线 ![]() 交于A,B两点. 求证:AC=BD.
交于A,B两点. 求证:AC=BD.
(3)知识应用:
如图3,反比例函数 ![]() (x>0)的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴,y轴分别交于点F,G .若矩形ABCO的面积为10,△ODG与△ODF的面积比为3:5,则k=________.
(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴,y轴分别交于点F,G .若矩形ABCO的面积为10,△ODG与△ODF的面积比为3:5,则k=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户要改造部分农田种植蔬菜.经调查,改造农田费用(元)与改造面积(亩)成正比,比例系数为900,添加辅助设备费用(元)与改造面积(亩)的平方成正比,比例系数为18,以上两项费用三年内不需再投入;每亩种植蔬菜还需种子、人工费用600元.这项费用每年均需再投入.除上述费用外,没有其他费用.设改造![]() 亩,每亩蔬菜年销售额为
亩,每亩蔬菜年销售额为![]() 元.
元.
(1)设改造当年收益为![]() 元,用含
元,用含![]() ,
,![]() 的式子表示
的式子表示![]() ;
;
(2)按前三年计算,若![]() ,是否改造面积越大收益越大?改造面积为多少时,可以得到最大收益?
,是否改造面积越大收益越大?改造面积为多少时,可以得到最大收益?
(3)按前三年计算,若![]() ,当收益不低于43200元时,求改造面积
,当收益不低于43200元时,求改造面积![]() 的取值范围.
的取值范围.
注:收益![]() 销售额
销售额![]() (改造费
(改造费![]() 辅助设备费
辅助设备费![]() 种子、人工费).
种子、人工费).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
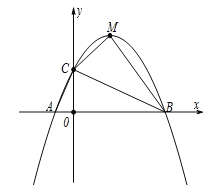
【题目】如图,已知抛物线![]() 交x轴于A、B两点(点A在点B的左侧),与y轴交于点C.
交x轴于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A、B、C的坐标;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
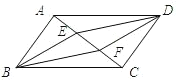
【题目】如图,四边形ABCD是平行四边形,![]() //
//![]() ,且分别交对角线AC于点E,F,连接BE,DF.
,且分别交对角线AC于点E,F,连接BE,DF.
(1)求证:AE=CF;
(2)若BE=DE,求证:四边形EBFD为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.
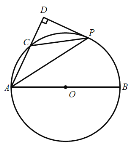
(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com