
【题目】市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表

兴趣班 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
| |
合计 |
|
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() _____,
_____,![]() ;
;
(2)根据调查结果,请你估计该市![]() 名小学生中最喜欢“绘画”兴趣班的人数;
名小学生中最喜欢“绘画”兴趣班的人数;
(3)王强和李昊选择参加兴趣班,若王强从![]() 三类兴趣班中随机选取一类,李吴从
三类兴趣班中随机选取一类,李吴从![]() 三类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类兴趣班的概率.
三类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类兴趣班的概率.
【答案】(1)18,0.24;(2)最喜欢“绘画”兴趣班的人数为![]() 人;(3)
人;(3)![]()
【解析】
(1)根据公式“频率=频数÷总数”,利用兴趣班B的频率、频数求得总数,再求得![]() 的值;
的值;
(2)总人数乘以A选项对应频率可得;
(3)根据题意画树状图,求出所有等可能的结果,再用两人恰好选中同一类的结果数除以总的结果数即可.
(1)兴趣班B的频率、频数分别为:15、0.3,
总数为:15![]() (人),
(人),
∴![]() 故答案为:18,0.24;
故答案为:18,0.24;
(2)估计该市4000名小学生中最喜欢“绘画”兴趣班的人数:4000×0.36=1440(人);
(3)画树状图:

由树状图可知共有![]() 种等可能情形,其中满足两人恰好两人恰好选中同一类兴趣班的有
种等可能情形,其中满足两人恰好两人恰好选中同一类兴趣班的有![]() 种,
种,
∴P(两人恰好选中同一类兴趣班)![]() .
.


科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.
(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB=∠GHC;
(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.
①依题意补全图形;
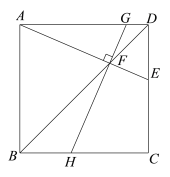

图1 备用图
②用等式表示线段AE与CN之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2020B2020C2020D2020的边长是( )
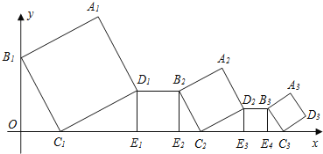
A.(![]() )2017B.(
)2017B.(![]() )2018C.(
)2018C.(![]() )2019D.(
)2019D.(![]() )2020
)2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与x轴、y轴相交于点B、C,经过点B、C的抛物线
分别与x轴、y轴相交于点B、C,经过点B、C的抛物线![]() 与x轴的另一个交点为A(-1,0).
与x轴的另一个交点为A(-1,0).
(1)求这个抛物线的表达式;
(2)已知点D在抛物线上,且横坐标为2,求出△BCD的面积;
(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于x轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,F为DA上一点,连接BF,E为BF中点,CD=6,sin∠ADB=![]() ,若△AEF的周长为18,则S△BOE=_____.
,若△AEF的周长为18,则S△BOE=_____.
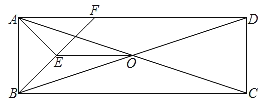
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为6,点E为AC边上一点,AE=2,作DE⊥AC于点E交AB于点D,点F在BC边上且BF=BD.连接EF与CD交于点H,则DH的长为( )
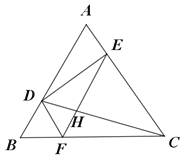
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别是DA、BC延长线上的点,且∠ABE=∠CDF.
求证:(1)△ABE≌△CDF;
(2)四边形EBFD是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com