
【题目】如图,某市有一块长为![]() 米,宽为
米,宽为![]() 米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为
米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为![]() 米的道路.(
米的道路.(![]() ).
).
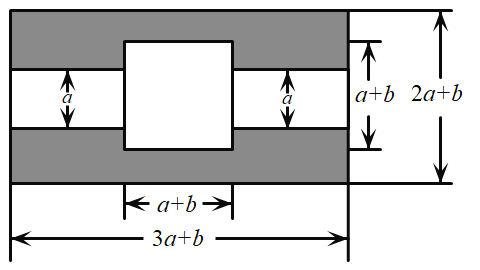
(1)①试用含![]() 的代数式表示绿化的面积是多少平方米?
的代数式表示绿化的面积是多少平方米?
②假设阴影部分可以拼成一个矩形.请你求出所拼矩形相邻两边的长:如果要使所拼矩形面积最大,求![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)若![]() ,请求出绿化面积.
,请求出绿化面积.
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】张老师将“校园诗词大赛”所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
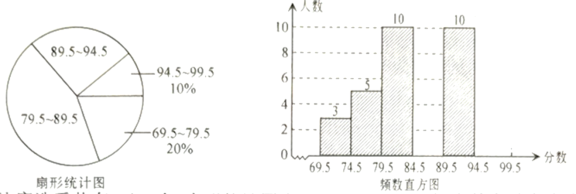
(1)本次比赛选手共有_ 人,扇形统计图中“![]() ”这一组人数占总参赛人数的百分比为_ ,频数直方图中“
”这一组人数占总参赛人数的百分比为_ ,频数直方图中“![]() ”这一组的人数为__ ;
”这一组的人数为__ ;
(2)赛前规定,成绩由高到低前![]() 的参赛选手获奖某参赛选手的比赛成绩为
的参赛选手获奖某参赛选手的比赛成绩为![]() 分,试判断他能否获奖,并说明理由;
分,试判断他能否获奖,并说明理由;
(3)成绩前四名是![]() 名男生和
名男生和![]() 名女生,若从他们中任选
名女生,若从他们中任选![]() 人作为全区“诗词大会”重点培训对象,试求恰好选中
人作为全区“诗词大会”重点培训对象,试求恰好选中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.
(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB=∠GHC;
(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.
①依题意补全图形;
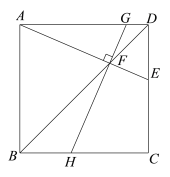

图1 备用图
②用等式表示线段AE与CN之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
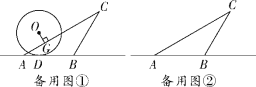
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半径为2的
,半径为2的![]() 从点
从点![]() 开始(如图①)沿直线
开始(如图①)沿直线![]() 向右滚动,滚动时始终与直线
向右滚动,滚动时始终与直线![]() 相切(切点为
相切(切点为![]() ),当
),当![]() 与
与![]() 只有一个公共点时滚动停止.作
只有一个公共点时滚动停止.作![]() 于点
于点![]() .
.
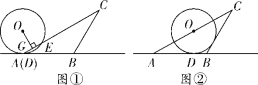
(1)图①中,![]() 在
在![]() 边上截得的弦长
边上截得的弦长![]() ______;
______;
(2)当圆心落在![]() 上时,如图②,判断
上时,如图②,判断![]() 与
与![]() 的位置关系,请说明理由;
的位置关系,请说明理由;
(3)在![]() 滚动过程中,线段
滚动过程中,线段![]() 的长度随之变化,设
的长度随之变化,设![]() ,
,![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并直接写出
之间的函数关系式,并直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
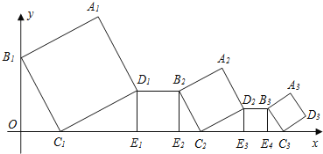
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2020B2020C2020D2020的边长是( )
A.(![]() )2017B.(
)2017B.(![]() )2018C.(
)2018C.(![]() )2019D.(
)2019D.(![]() )2020
)2020
查看答案和解析>>
科目:初中数学 来源: 题型:
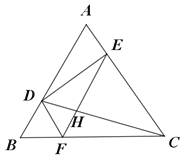
【题目】如图,等边三角形ABC的边长为6,点E为AC边上一点,AE=2,作DE⊥AC于点E交AB于点D,点F在BC边上且BF=BD.连接EF与CD交于点H,则DH的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com