
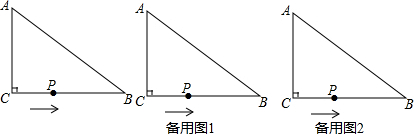
���� ��1�������ٶ�Ϊÿ��2cm���������2���CP�ij���Ȼ����������ʽ���ɵõ������
��2����ͼ1���ɹ��ɶ����õ�AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10��������֪�����õ���ACP�ա�ADP�����ǵõ�AD=AC=6cm��BD=AB-AD=4cm�����ݹ��ɶ����з��̼��ɵõ����ۣ�
��3������ͼ2����P�ڱ�BC��ʱ��AC=CP=6cm����ʱ�õ�ʱ��Ϊ3s����ACPΪ���������Σ�
����P��AB����ʱ���������������i����ʹAP=CA=6cm����ʱBP=4cm��P�˶���·��Ϊ8+4=12cm�������õ�ʱ��Ϊ6s����BCPΪ���������Σ�ii����CP=AC=6cm����C��б��AB�ĸߣ������������ø�Ϊ4.8cm����CD��AB�ڵ�D����Rt��PCD�У�PD=3.6������AP=2PD=7.2cm������P�˶���·��Ϊ18-7.2=10.8cm�����õ�ʱ��Ϊ5.4s��ACPΪ���������Σ�������AP=CP����ʱPӦ��Ϊб��AB���е㣬P�˶���·��Ϊ8+5=13cm�������õ�ʱ��Ϊ6.5s����ACPΪ���������Σ�
��� �⣺��1����AC=6cm��PC=2��2=4cm��
��S��ABC=$\frac{1}{2}$AC•PC=$\frac{1}{2}��6��4$=12cm2��
��2����ͼ1���ߡ�C=90�㣬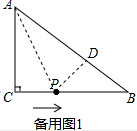
��AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10��
��������ã���ACP�ա�ADP��
��AD=AC=6cm��BD=AB-AD=4cm��
PD=PC=2t��
��PB=8-2t��
��Rt��PDB��PD2+BD2=PB2��
�ࣨ2t��2+42=��8-2t��2��
��ã�t=1.5��
��3������ͼ2����P�ڱ�BC��ʱ��AC=CP=6cm��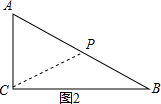
��ʱ�õ�ʱ��Ϊ3s����ACPΪ���������Σ�
����P��AB����ʱ�������������
��i����ͼ3��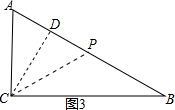
��ʹAP=CA=6cm����ʱBP=4cm��P�˶���·��Ϊ8+4=12cm��
�����õ�ʱ��Ϊ6s����BCPΪ���������Σ�
ii����ͼ4��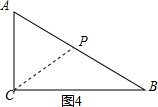
��CP=AC=6cm����C��б��AB�ĸߣ������������ø�Ϊ4.8cm��
��CD��AB�ڵ�D��
��Rt��PCD��PD=3.6��
����AP=2PD=7.2cm��
����P�˶���·��Ϊ18-7.2=10.8cm��
���õ�ʱ��Ϊ5.4s����ACPΪ���������Σ�
������ͼ5��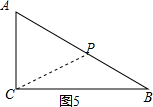
��AP=CP����ʱPӦ��Ϊб��AB���е㣬P�˶���·��Ϊ8+5=13cm
�����õ�ʱ��Ϊ6.5s����ACPΪ���������Σ�
������������tΪ3s��5.4s��6s��6.5sʱ����ACPΪ���������Σ�
���� ���⿼���˵��������ε��ж������һ������������������ȣ���ô�����������Եı�Ҳ��ȣ�Ҳ�����˹��ɶ����ͷ������۵�˼�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
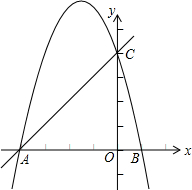 ��ͼ��������y=ax2-bx-4a��x���ڵ�A��B����y���ڵ�C�����е�B��C������ֱ�ΪB��1��0����C��0��4����
��ͼ��������y=ax2-bx-4a��x���ڵ�A��B����y���ڵ�C�����е�B��C������ֱ�ΪB��1��0����C��0��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
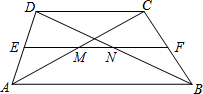 ��ͼ��������ABCD��AB��CD����λ��EF��Խ���AC��BD����M��N���㣬��EF=18��NM=8����AB��Ϊ��������
��ͼ��������ABCD��AB��CD����λ��EF��Խ���AC��BD����M��N���㣬��EF=18��NM=8����AB��Ϊ��������| A�� | 10 | B�� | 13 | C�� | 20 | D�� | 26 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
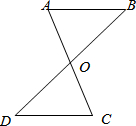 ��ͼ����֪AC��BD�ཻ�ڵ�O��AO=CO��BO=DO����AB=CD����˵�����ɣ�
��ͼ����֪AC��BD�ཻ�ڵ�O��AO=CO��BO=DO����AB=CD����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
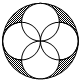 ��ͼ���ĸ��뾶Ϊ1��СԲ������ԲԲ�������Բ�����У�����Ӱ���ֵ����Ϊ2��-4��
��ͼ���ĸ��뾶Ϊ1��СԲ������ԲԲ�������Բ�����У�����Ӱ���ֵ����Ϊ2��-4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
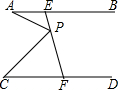 ��ͼ����֪AB��CD���߶�EF�ֱ���AB��CD�ཻ�ڵ�E��F��PΪ�߶�EF�ϵ�һ�㣬����AP��CP������A=25�㣬��APC=70�㣬���C�Ķ���Ϊ��������
��ͼ����֪AB��CD���߶�EF�ֱ���AB��CD�ཻ�ڵ�E��F��PΪ�߶�EF�ϵ�һ�㣬����AP��CP������A=25�㣬��APC=70�㣬���C�Ķ���Ϊ��������| A�� | 45�� | B�� | 40�� | C�� | 35�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��Ԫ�� | 20 | 30 | 35 | 50 | 100 |
| ѧ�������ˣ� | 3 | 6 | 6 | 15 | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
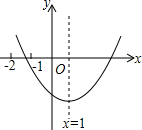 ��֪���κ���y=ax2+bx+c��a��0���ٵ�ͼ����ͼ��ʾ���������½��ۣ���b2��4ac����abc��0����2a-b=0����8a+c��0����9a+3b+c��0�����н�����ȷ�ĸ����У�������
��֪���κ���y=ax2+bx+c��a��0���ٵ�ͼ����ͼ��ʾ���������½��ۣ���b2��4ac����abc��0����2a-b=0����8a+c��0����9a+3b+c��0�����н�����ȷ�ĸ����У�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com