
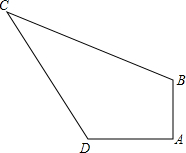
 有一块四边形的花坛ABCD,其中AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求这块花坛的面积.
有一块四边形的花坛ABCD,其中AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求这块花坛的面积. 分析 连接BD,由勾股定理求出BD,再由勾股定理的逆定理求出∠BDC=90°,这块花坛的面积=△ABD的面积+△BDC的面积,即可得出结果.
解答 解:连接BD,如图所示: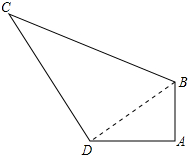
∵∠A=90°,
∴△ABD的面积=$\frac{1}{2}$AD•AB=$\frac{1}{2}$×4×3=6(cm2),
BD2=AB2+AD2=32+42=52,
∴BD=5,
∵52+122=132,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴△BDC的面积=$\frac{1}{2}$BD•CD=$\frac{1}{2}$×5×12=30(cm2),
∴这块花坛的面积=△ABD的面积+△BDC的面积=36cm2.
点评 本题考查了勾股定理、勾股定理的逆定理、三角形面积的计算;熟练掌握勾股定理和勾股定理的逆定理,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 国家规定“中小学生每天在校体育活动时间不低于1h”,为此,某市就“每天在校体育活动”时间的问题随机调查了辖区内320名初中学生,根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
国家规定“中小学生每天在校体育活动时间不低于1h”,为此,某市就“每天在校体育活动”时间的问题随机调查了辖区内320名初中学生,根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
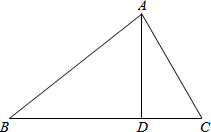 如图所示,在△ABC中,点D为BC边上的一点,AD=12,BD=16,AB=20,CD=9.
如图所示,在△ABC中,点D为BC边上的一点,AD=12,BD=16,AB=20,CD=9.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com