
【题目】如图,在平面直角坐标系中,已知![]() ,其中a,b满足
,其中a,b满足![]()

(1)填空:a= ,b= ;
(2)如果在第三象限内有一点C(-2,m),请用含m的式子表示△ABC的面积;
(3)在⑵条件下,当![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
【答案】(1)-1,3;(2)-2m;(3)(0,0.3)或(0,-2.1).
【解析】
(1)根据非负数性质可得a、b的值;
(2)根据三角形面积公式列式整理即可;
(3)先根据(2)计算S△ABM,再分两种情况:当点P在y轴正半轴上时、当点P在y轴负半轴上时,利用割补法表示出S△BMP,根据S△BMP=S△ABM列方程求解可得.
解:(1)∵|a+1|+(b-3)2=0,
∴a+1=0且b-3=0,
解得:a=-1,b=3,
故答案为:-1,3;
(2)过点M作MN⊥x轴于点N,
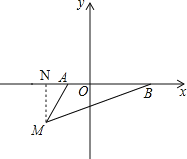
∵A(-1,0),B(3,0),
∴AB=1+3=4,
又∵点M(-2,m)在第三象限
∴MN=|m|=-m
∴S△ABM=![]() ABMN=
ABMN=![]() ×4×(-m)=-2m;
×4×(-m)=-2m;
(3)当m=-![]() 时,M(-2,-
时,M(-2,-![]() )
)
∴S△ABM=-2×(-![]() )=3,
)=3,
点P有两种情况:①当点P在y轴正半轴上时,设点p(0,k)
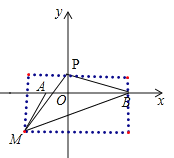
S△BMP=5×(![]() +k)-
+k)-![]() ×2×(
×2×(![]() +k)-
+k)-![]() ×5×
×5×![]() -
-![]() ×3×k=
×3×k=![]() k+
k+![]() ,
,
∵S△BMP=S△ABM,
∴![]() k+
k+![]() =3,
=3,
∴点P坐标为(0,0.3);
②当点P在y轴负半轴上时,设点p(0,n),
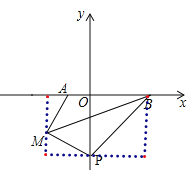
S△BMP=-5n-![]() ×2×(-n-
×2×(-n-![]() )-
)-![]() ×5×
×5×![]() -
-![]() ×3×(-n)=-
×3×(-n)=-![]() n-
n-![]() ,
,
∵S△BMP=S△ABM,
∴-![]() n-
n-![]() =3,
=3,
解得:n=-2.1,
∴点P坐标为(0,-2.1),
故点P的坐标为(0,0.3)或(0,-2.1).


科目:初中数学 来源: 题型:
【题目】某中学在今年4月23日的“世界读书日”开展“人人喜爱阅读,争当阅读能手”活动,同学们积极响应,涌现出大批的阅读能手.为了激励同学们的阅读热情,养成每天阅读的好习惯,学校对阅读能手进行了奖励表彰,计划用2700元来购买甲、乙、丙三种书籍共100本作为奖品,已知甲、乙、丙三种书的价格比为2:2:3,甲种书每本20元.
(1)求出乙、丙两种书的每本各多少元?
(2)若学校购买甲种书的数量是乙种书的1.5倍,恰好用完计划资金,求甲、乙、丙三种书各买了多少本?
(3)在活动中,同学们表现优秀,学校决定提升奖励档次,增加了245元的购书款,在购买书籍总数不变的情况下,求丙种书最多可以买多少本?
(4)七(1)班阅读氛围浓厚,同伴之间交换书籍共享阅读,已知甲种书籍共270页,小明同学阅读甲种书籍每天21页,阅读5天后,发现同伴比他看得快,为了和同伴及时交换书籍,接下来小明每天多读了a页(20<a<40),结果再用了b天读完,求小明读完整本书共用了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】许多代数恒等式可以借助图形的面积关系直观表达,如图①,根据图中面积关系可以得到:![]() 。
。

(1)如图②,根据图中面积关系,写出一个关于![]() 的等式 ;
的等式 ;
(2)利用(1)中的等式求解:![]() ,则
,则![]() ;
;
(3)小明用8个面积一样大的长方形(宽![]() ,长
,长![]() )拼图,拼出了如图甲、乙的两种图案;图案甲是一个大的正方形,中间阴影部分是边长为3的小正方形;图案乙是一个大的长方形,求
)拼图,拼出了如图甲、乙的两种图案;图案甲是一个大的正方形,中间阴影部分是边长为3的小正方形;图案乙是一个大的长方形,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点A﹙2,4﹚、C﹙4,n﹚,交y轴于点B,交x轴于点D.
的图像交于点A﹙2,4﹚、C﹙4,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2)连接OA、OC,求△AOC的面积;
(3)写出使一次函数的值大于反比例函数的![]() 的取值范围 .
的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形![]() 折叠,使
折叠,使![]() 落在对角线
落在对角线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 落在点
落在点![]() 处,若
处,若![]() ,则
,则![]() ;
;
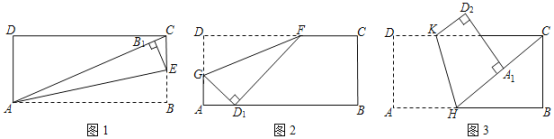
(2)小丽手中有一张矩形纸片,![]() ,
,![]() .她准备按如下两种方式进行折叠:
.她准备按如下两种方式进行折叠:
①如图2,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使点
上,将纸片折叠,使点![]() 落在边
落在边![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
②如图3,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() ,
,![]() 分别落在
分别落在![]() ,
,![]() 处,若
处,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).

(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿BC→CD移动.若点P的速度为每秒1个单位长度,运动时间为t秒,请解决以下问题,并说明你的理由:
①当t为多少秒时,点P的横坐标与纵坐标互为相反数;
②在运动过程中的坐标(用含t的式子表示)
③当3秒<t<5秒时,设∠CBP=![]() ,∠PAD=
,∠PAD=![]() ,∠BPA=
,∠BPA=![]() ,试问
,试问![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“英语口语听力”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,81,82,85,83 乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是 ,乙成绩的平均数是 ;
(2)求甲、乙两名同学测试成绩的方差S甲2与S乙2.
(3)请你选择一个角度来判断选拔谁参加比赛更合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点C、D分别在边OA、OB上的点.连接AD,BC,点H为BC中点,连接OH.


(1)如图1,求证:OH=![]() AD,OH⊥AD;
AD,OH⊥AD;
(2)将△COD绕点O旋转到图2所示位置时,⑴中结论是否仍成立?若成立,证明你的结论;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现任意三个连续的整数中,最大数与最小数这两个数的平方差是4的倍数;
验证:(1) ![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续的整数中间的一个为n,计算最大数与最小数这两个数的平方差,并说明它是4的倍数;
延伸:说明任意三个连续的奇数中,最大的数与最小的数这两个数的平方差是8的倍数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com