
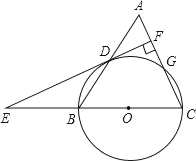
【题目】如图,在等腰△ABC中,AC=BC=10,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC于F,交CB的延长线于点E.
(1)求证:直线EF是⊙O的切线;
(2)若sin∠E=![]() ,求AB的长.
,求AB的长.
【答案】(1)见解析;(2)AB=2![]() .
.
【解析】
(1)连接OD,根据等腰三角形性质求出∠A=∠ABC=∠ODB,推出OD∥AC,推出OD⊥DF,根据切线判定推出即可;
(2)连接BG,推出BG∥EF,推出∠E=∠GBC,根据已知推出sin∠GBC=![]() =
=![]() ,求出CG,求出AG,根据勾股定理求出BG,在△BGA中,根据勾股定理求出AB即可.
,求出CG,求出AG,根据勾股定理求出BG,在△BGA中,根据勾股定理求出AB即可.
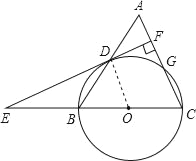
(1)证明:连接OD,
∵AC=BC,
∴∠ABC=∠BAC,
∵OD=OB,
∴∠ABC=∠ODB,
∴∠BAC=∠BDO,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∵OD为半径,
∴直线EF是⊙O的切线;
(2)连接BG,

∵BC是⊙O直径,
∴∠BGC=90°,
∵DF⊥AC,
∴∠DFC=90°=∠BGC,
∴BG∥EF,
∴∠E=∠GBC,
∵sin∠E=![]() ,
,
∴sin∠GBC=![]() =
=![]() ,
,
∵BC=10,
∴CG=4,
∴AG=10﹣4=6,由勾股定理得:BG=![]() ,
,
在Rt△BGA中,由勾股定理得:AB=![]() ,即AB=2
,即AB=2![]() .
.


科目:初中数学 来源: 题型:
【题目】5月12日是母亲节,小明去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支5元,兰花每支3元,小明只有30元,希望购买花的支数不少于7支,其中至少有一支是康乃馨.
(1)小明一共有多少种可能的购买方案?列出所有方案;
(2)如果小明先购买一张2元的祝福卡,再从(1)中任选一种方案购花,求他能实现购买愿望的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
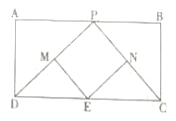
【题目】如图,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点.
的中点.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形,说明理由.
是菱形,说明理由.
(3)四边形![]() 有可能是矩形吗?若有可能,求出
有可能是矩形吗?若有可能,求出![]() 的长;若不可能,请说明理由.
的长;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
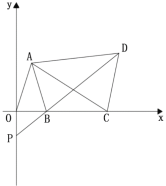
【题目】如图,平面直角坐标系中,已知点![]() 且
且![]() 为
为![]() 轴上点
轴上点![]() 右侧的动点,以
右侧的动点,以![]() 为腰作等腰
为腰作等腰![]() ,使
,使![]() 直线
直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当点![]() 运动时,点
运动时,点![]() 在
在![]() 轴上的位置是否发生改变,为什么?
轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PD=2,下列结论:①EB⊥ED;②∠AEB=135°;③S正方形ABCD=5+2![]() ;④PB=2;其中正确结论的序号是( )
;④PB=2;其中正确结论的序号是( )

A.①③④B.②③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第一象限,⊙A与x轴交于B(2,0)、C(8,0)两点,与y轴相切于点D,则点A的坐标是( )
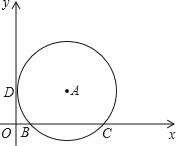
A. (5,4) B. (4,5) C. (5,3) D. (3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题探究】
(![]() )如图①,点
)如图①,点![]() 是正
是正![]() 高
高![]() 上的一定点,请在
上的一定点,请在![]() 上找一点
上找一点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
(![]() )如图②,点
)如图②,点![]() 是边长为
是边长为![]() 的正
的正![]() 高
高![]() 上的一动点,求
上的一动点,求![]() 的最小值.
的最小值.
【问题解决】
(![]() )如图③,
)如图③,![]() 、
、![]() 两地相距
两地相距![]() ,
, ![]() 是笔直第沿东西方向向两边延伸的一条铁路.今计划在铁路线
是笔直第沿东西方向向两边延伸的一条铁路.今计划在铁路线![]() 上修一个中转站
上修一个中转站![]() ,再在
,再在![]() 间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由
间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由![]() 到
到![]() 再通过公路由
再通过公路由![]() 到
到![]() 的总运费达到最小值,请确定中转站
的总运费达到最小值,请确定中转站![]() \的位置,并求出
\的位置,并求出![]() 的长.(结果保留根号)
的长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
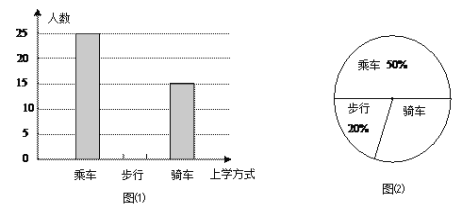
【题目】学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)求该班共有多少名学生;
(2)在图(1)中,将表示“步行”的部分补充完整;
(3)在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数;
(4)如果全年级共600名同学,请你估算全年级步行上学的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
⑴先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为_______,若A为随机事件,则m的取值为______;
⑵若从袋中随机摸出2个球,正好红球、黑球各1个,用列表法与树状图法求这个事件的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com