
分析 (1)要证明方程有两个不相等的实数根,即证明△>0即可.△=(k+1)2-4(-k-3)=k2+6k+13=(k+3)2+4,因为(k+3)2≥0,可以得到△>0;
(2)将x=2代入方程x2+(k+1)x-k-3=0,求出k的值,进而得出方程的解.
解答 (1)证明:∵△=(k+1)2-4(-k-3)=k2+6k+13=(k+3)2+4,
而(k+3)2≥0,
∴△>0.
∴对任意实数k,方程有两个不相等的实数根;
(2)解:∵方程的一个根是2,
∴22+2(k+1)-k-3=0,
解得:k=-3,
∴原方程为:x2-2x=0,
解得:x1=2,x2=0.
方程的另一个根是0.
点评 此题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.同时考查了一元二次方程的解的定义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
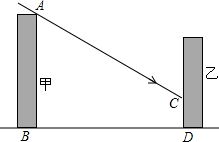 如图,在我国北方某居民区有一座甲楼,坐落在正南正北方向,楼高16米,要在甲楼的北面建一座乙楼,已知冬至这一天正午时太阳光线与水平线的夹角是32°.
如图,在我国北方某居民区有一座甲楼,坐落在正南正北方向,楼高16米,要在甲楼的北面建一座乙楼,已知冬至这一天正午时太阳光线与水平线的夹角是32°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com