
分析 利用多项式的定义以及二元一次方程组的解法得出x,y的值,进而得出答案.
解答 解:代数式3x2y-3xy2-x3+y3按x升幂排列为:y3-3xy2+3x2y-x3,
∵3ax-yb3与-5ab2x+y的和仍是单项式,
∴$\left\{\begin{array}{l}{x-y=1}\\{2x+y=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=\frac{1}{3}}\end{array}\right.$,
则3x2y-3xy2-x3+y3
=3×($\frac{4}{3}$)2×$\frac{1}{3}$-3×$\frac{4}{3}$×($\frac{1}{3}$)2-($\frac{4}{3}$)3+($\frac{1}{3}$)3
=-1.
点评 此题主要考查了同类项以及多项式,根据合并同类项法则得出x,y的值是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
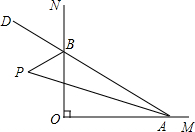 如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么?
如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com