
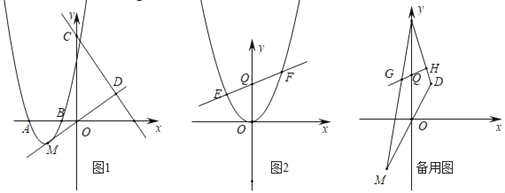
����Ŀ����ͼ1��������y��ax2+bx+3������A(��3��0)��B(��1��0)���㣬�����ߵĶ���ΪM��ֱ��y����4x+9��y�ύ�ڵ�C����ֱ��OM���ڵ�D��
(1)�������ߵĽ���ʽ��
(2)��Q(0��3)����ƽ����x���ֱ��l
����ͼ2����������ƽ�ƣ���������ԭ��ʱ��ֱ��l���������ڵ�E��F����y���ϴ���һ��P��ʹ��PEF��������y���ϣ����P�����ꣻ
��ֱ��l����CMD�ı�CM��CD�ڵ�G��H(G�㲻��M���غϡ�H�㲻��D���غ�)��S�ı���MDHG��S��CGH�ֱ��ʾ�ı���MDHG�͡�CGH���������̽��![]() �����ֵ��
�����ֵ��
���𰸡�(1)�����ߵĽ���ʽΪy��x2+4x+3��(2)�ٵ�P����Ϊ(0����3)���ڵ�x��![]() ʱ��
ʱ�� ![]() �����ֵ�����ֵΪ
�����ֵ�����ֵΪ![]() ��
��
��������
��1����A��3��0����B��1��0�����������߽���ʽ�����ô���ϵ����������⣻
��2���ٷֱ�д��������ƽ�ƺ�Ľ���ʽ��ֱ��EF�Ľ���ʽ����P��GH��x�ᣬ�ֱ��E��F��GH�Ĵ��ߣ�����ֱ�ΪG��H�������ĵ����ʵýǵȣ����������������ε����ʿɽ⣻
������OG���ɵ�C�͵�Q�����꣬��CQ����2OQ���ɵ�M�͵�D���꣬��MO����OD���ֱ���������GQO�������ʾ��������CGQ��������CGO�������
����CG��1��MG��x���ú�x��ʽ�ӱ�ʾ����������κ��ı���MDHG����������Ҫ��ı�ֵת��Ϊ����x�Ķ��κ������Ӷ��ɽ⣮
(1)��������y��ax2+bx+3������A(��3��0)��B(��1��0)���㣬
��![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy��x2+4x+3��
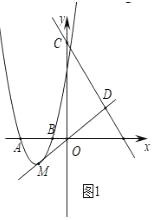
(2)�ٽ�������ƽ�ƣ���������ԭ��ʱ�������ʽΪy��x2��
��EF����(0��3)�����������ʽΪy��kx+3(k��0)��
�����������ص�P����Ϊ(0��t)��
��ͼ����P��GH��x�ᣬ�ֱ��E��F��GH�Ĵ��ߣ�����ֱ�ΪG��H��
�ߡ�PEF��������y���ϣ�
���GEP����EPQ����QPF����HFP��
���GEP�ס�HFP��
��![]() ��
��
��![]() ��
��
��2![]() xF��(t��3)(xE+xF)��
xF��(t��3)(xE+xF)��
��y��x2��y����kx+3��x2��kx��3��0��
��xE+xF��k��xExF����3��
��2k(��3)��(t��3)k
��k��0����t����3��
���P����Ϊ(0����3)��

����ͼ������OG��
��C(0��9)Q(0��3)��
��CQ��2OQ��
�֡�M(��2����1)��D(2��1)��
��MO��OD��
��S��GQO��S��
��S��CGQ��2S��S��CGO��3S��
������CG��1��MG��x����S��MGO��3xS��
��S��CMO��S��CQO+S��MGO��3S+3xS��(3x+3)S��
��S��CMD��2S��CMO��(6x+6)S��
��QH��kQG����S��CGQ��2S����S��CQH��2kS��
��S��CGH��(2k+2)S��
��S�ı���MDHG��(6x+6)S��(2k+2)S��(6x��2k+4)S��
��![]() ��
��![]() ����
����
����Q��QK��MD����CD�ڵ�K������G��GN��MD����CD�ڵ�N����QK��GN��
��![]() ��
��
��QK��![]() OD��
OD��![]() MD��
MD��
��GN��MD��
��![]() ��
��
�� ��
��
��![]() ��
��
��QK��GN��
��![]() ��
��
��![]() ��
��
��k��![]() ��
��
�����ʽ�ã�![]() ��
��![]() ��
�� ����x2+x+1��
����x2+x+1��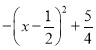 ��
��
�൱x��![]() ʱ��
ʱ�� ![]() �����ֵ�����ֵΪ
�����ֵ�����ֵΪ![]() ��
��



 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г߹���ͼ�У���ȷ��Բ�ĵ��ǣ�������
����ͼ1����Բ����ȡ������A��B��C���ֱ�����AB��BC�Ĵ�ֱƽ���ߣ�����O��ΪԲ��
����ͼ2����Բ����ȡһ��B����BΪԲ�ģ�С��ֱ����Ϊ�뾶������Բ��A��C��������AB��BC������ABC��ƽ���߽�Բ�ڵ�D������BD�Ĵ�ֱƽ���߽�BD�ڵ�O����O��ΪԲ��
����ͼ3����Բ�Ͻ�ȡ��AB��CD������AB��BC��CD���ֱ�����ABC���DCB��ƽ���ߣ�����O��ΪԲ��

A. �٢�B. �٢�C. �ڢ�D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
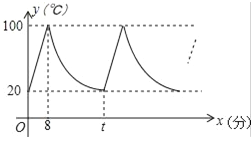
����Ŀ��С������ˮ����ԭ��ˮ���¶�Ϊ20�棬ͨ�翪������ˮ���Զ���ʼ����[�˹�����ˮ��y���棩�뿪��ʱ��x���֣�����һ�κ�����ϵ]�������ȵ�100��ʱ�Զ�ֹͣ���ȣ����ˮ�¿�ʼ�½�[�˹�����ˮ��y���棩�뿪��ʱ��x���֣��ɷ�������ϵ]����ˮ�½���20��ʱ����ˮ�����Զ���ʼ���ȡ����ظ�����������ͼ��ʾ��������ͼ���ṩ����Ϣ������������⣺
��1����0��x��8ʱ����ˮ��y���棩�뿪��ʱ��x���֣��ĺ�����ϵʽ��
��2����ͼ��t��ֵ��
��3����С����ͨ�翪�������ɢ��������Ԥ��С��ɢ��45���ӻص���ʱ����ˮ���ڵ��¶�ԼΪ���١棿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
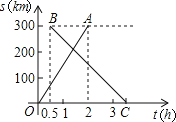
����Ŀ��������̨��������֮�俪ͨ�˶���������г�����֪ÿ��1h��һ���ٶ���ͬ�Ķ������г�����������̨�ݣ���ͼ��ʾ��OA�ǵ�һ�ж������г��뿪������·��s(��λ��km)������ʱ��t(��λ��h)�ĺ���ͼ��BC��һ�д�̨�ݿ�����������ͨ�쳵��������·��s(��λ��km)������ʱ��t(��λ��h)�ĺ���ͼ�������ͼ����Ϣ������������⣺
(1)��B������0.5����������ͨ�쳵�ķ���ʱ��ȵ�һ�ж������г��ķ���ʱ������ ��h����B��������300���������� ����
(2)����ͨ�г����ٶ�Ϊ100km/h��
����BC�Ľ���ʽ��
����ڶ��ж������г�������ʱ������ͨ�г�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������������ؿ���Ŀ��Ϊ��ijѧУ���С������������ԣ����ɼ�10�֡�9�֡�8�֡�7�֣���Ӧ��ΪA��B��C��D�ĸ��ȼ���ij����ݲ��Գɼ���������ͳ��ͼ����ش��������⣺
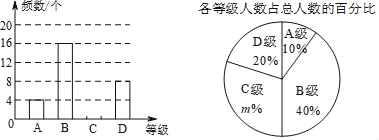
(1)�ð༶��������Ϊ�� ����m���� ����
(2)��ȫ����ͳ��ͼ��
(3)�ðࡰ���������Ե�ƽ���ɼ��Ƕ��٣�
(4)�����ӵȼ�ΪA��4����(2��2Ů)�������ȡ������ȥ�μӱ����������б�����״ͼ�ķ��������ǡ�ó鵽һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�DEƽ�֡�ADB����AB��E��BFƽ�֡�CBD����CD��F��
��1����֤����ADE�ա�CBF��
��2����AD��BD����ʲô��ϵʱ���ı���DEBF�Ǿ��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ѳ�����ֽƬABCD�ضԽ����۵������ص�����Ϊ��EBD����ô��������˵�����١�EBD�ǵ��������Σ�EB��ED�����۵����ABE�͡�CBDһ����ȣ����۵���õ���ͼ������Գ�ͼ�Σ��ܡ�EBA�͡�EDCһ����ȫ�������Σ�������ȷ����( )

A. �٢ڢ�B. �٢ۢ�C. �٢ڢ�D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
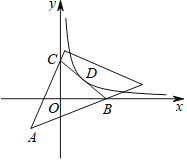
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ������45���ǵ����ǰ������һ����Ƕ������ڵ�A����3����3�����������Ƶ�A��ת�����45���ǵ��������ڵ�ֱ�߷ֱ�x�ᡢy����������ڵ�B��C������BC������![]() ��x��0����ͼ��BC���е�D����k��_____��
��x��0����ͼ��BC���е�D����k��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ���ڵġ�MAN�����ڲ���һ��P�����P��ֱ��AM��AN�ľ���ֱ�Ϊd1��d2����![]() ��
��![]() ���������нϴ��һ��Ϊ��P����
���������нϴ��һ��Ϊ��P����![]() �ġ�ƫ�ʡ� . ��ƽ��ֱ������ϵxOy�У�
�ġ�ƫ�ʡ� . ��ƽ��ֱ������ϵxOy�У�
��1����M��N�ֱ�Ϊx�������ᣬy���������ϵ�������.
������P������Ϊ��1��5�������P����![]() �ġ�ƫ�ʡ�Ϊ____________��
�ġ�ƫ�ʡ�Ϊ____________��
������һ�����ڵ�Q��a��b������![]() �ġ�ƫ�ʡ�Ϊ1����a��b����Ĺ�ϵΪ____________��
�ġ�ƫ�ʡ�Ϊ1����a��b����Ĺ�ϵΪ____________��
��2����֪��A��4��0����B��2��![]() ��������OB��AB����C���߶�AB��һ���㣨��C�����A��B�غϣ�. ����C����
��������OB��AB����C���߶�AB��һ���㣨��C�����A��B�غϣ�. ����C����![]() �ġ�ƫ�ʡ�Ϊ2�����C�����ꣻ
�ġ�ƫ�ʡ�Ϊ2�����C�����ꣻ
��3����E��F�ֱ�Ϊx�������ᣬy���������ϵ������㣬����T������Ϊ��t��4����![]() ���Ե�TΪԲ�ģ��뾶Ϊ1��Բ. ��
���Ե�TΪԲ�ģ��뾶Ϊ1��Բ. ��![]() �ϵ����е㶼�ڵ�һ���ޣ��ҹ���
�ϵ����е㶼�ڵ�һ���ޣ��ҹ���![]() �ġ�ƫ�ʡ�������
�ġ�ƫ�ʡ�������![]() ��ֱ��д��t��ȡֵ��Χ.
��ֱ��д��t��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com