
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:

小明的作法如下:

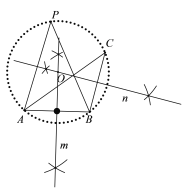
老师说:“小明的作法正确.”
请回答:(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是____;
(2)∠APB=∠ACB的依据是______________.
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=![]() 在第一象限内的图象与△ABC有交点,则k的取值范围是_____.
在第一象限内的图象与△ABC有交点,则k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 知识储备
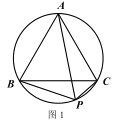
①如图 1,已知点 P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC= PA.
②定义:在△ABC 所在平面上存在一点 P,使它到三角形三顶点的距离之和最小,则称点 P 为△ABC
的费马点,此时 PA+PB+PC 的值为△ABC 的费马距离.
(2)知识迁移
①我们有如下探寻△ABC (其中∠A,∠B,∠C 均小于 120°)的费马点和费马距离的方法:
如图 2,在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆,根据(1)的结论,易知线段____的长度即为△ABC 的费马距离.
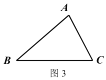
②在图 3 中,用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)知识应用
①判断题(正确的打√,错误的打×):
ⅰ.任意三角形的费马点有且只有一个(__________);
ⅱ.任意三角形的费马点一定在三角形的内部(__________).
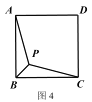
②已知正方形 ABCD,P 是正方形内部一点,且 PA+PB+PC 的最小值为![]() ,求正方形 ABCD 的
,求正方形 ABCD 的
边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
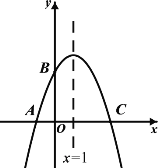
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴的一个交点为A(-1,0),对称轴为直线x =1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列四个结论中,①当x>3时,y<0;② 3a+b<0;③-1≤a ≤![]() ;④4ac-b2> 8a;所有正确结论的序号是_______________ .
;④4ac-b2> 8a;所有正确结论的序号是_______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,将抛物线在
,将抛物线在![]() 轴左侧部分沿
轴左侧部分沿![]() 轴翻折,翻折后的部分和抛物线与
轴翻折,翻折后的部分和抛物线与![]() 轴交点以及
轴交点以及![]() 轴右侧部分组成图形
轴右侧部分组成图形![]() ,已知
,已知![]()

(1)求抛物线![]() 的对称轴;
的对称轴;
(2)当![]() 时,
时,
①若点![]() 在图形
在图形![]() 上,求
上,求![]() 的值;
的值;
②直接写出线段![]() 与图形
与图形![]() 的公共点个数;
的公共点个数;
(3)当n<0时,若线段![]() 与图形
与图形![]() 恰有两个公共点,直接写出
恰有两个公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
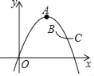
【题目】如图,曲线BC是反比例函数y=![]() (4≤x≤6)的一部分,其中B(4,1﹣m),C(6,﹣m),抛物线y=﹣x2+2bx的顶点记作A.
(4≤x≤6)的一部分,其中B(4,1﹣m),C(6,﹣m),抛物线y=﹣x2+2bx的顶点记作A.
(1)求k的值.
(2)判断点A是否可与点B重合;
(3)若抛物线与BC有交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,以BC为直径的半圆交AB于点D,O是该半圆所在圆的圆心,E为线段AC上一点,且ED=EA.
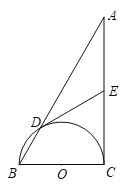
(1)求证:ED是⊙O的切线;
(2)若![]() ,∠A=30°,求⊙O的半径.
,∠A=30°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
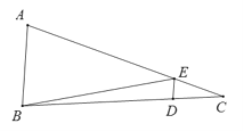
【题目】如图,在△ABC中,D、E分别是BC、AC上的点,且DE∥AB,若S△CDE :S△BDE=1:3,则S△CDE:S△ABE =( )
A.1:9B.1:12
C.1:16D.1:20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com