
【题目】已知抛物线![]() ,将抛物线在
,将抛物线在![]() 轴左侧部分沿
轴左侧部分沿![]() 轴翻折,翻折后的部分和抛物线与
轴翻折,翻折后的部分和抛物线与![]() 轴交点以及
轴交点以及![]() 轴右侧部分组成图形
轴右侧部分组成图形![]() ,已知
,已知![]()

(1)求抛物线![]() 的对称轴;
的对称轴;
(2)当![]() 时,
时,
①若点![]() 在图形
在图形![]() 上,求
上,求![]() 的值;
的值;
②直接写出线段![]() 与图形
与图形![]() 的公共点个数;
的公共点个数;
(3)当n<0时,若线段![]() 与图形
与图形![]() 恰有两个公共点,直接写出
恰有两个公共点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①5;②3;3)
;(2)①5;②3;3)![]()
【解析】
(1)根据抛物线的对称轴公式求解即可;
(2)①可先求出点A关于x轴的对称点,再代入已知的抛物线求解;②画出函数图象,结合函数图象即得答案;
(3)根据图象找出线段![]() 与图形
与图形![]() 恰有两个公共点和恰有一个公共点时对应的n的值,问题即得解决.
恰有两个公共点和恰有一个公共点时对应的n的值,问题即得解决.
解:(1)抛物线的对称轴是:直线![]() ;
;
(2)①当n=0时,![]() ,
,
∵A(-1,m)在图形G上,∴A(-1,m)关于x轴的对称点(―1,―m)在![]() 图象上,∴
图象上,∴![]() ,解得:m=5.
,解得:m=5.
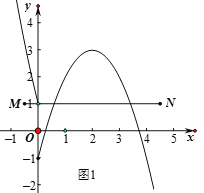
② ∵y轴左侧部分的解析式是![]() ,当
,当![]() 时,
时,![]() ,∴线段
,∴线段![]() 与图形
与图形![]() 的公共点个数是3个,如图.:
的公共点个数是3个,如图.:

(3)当线段![]() 与图形
与图形![]() 恰有两个公共点时,如图1,此时
恰有两个公共点时,如图1,此时![]() ,
,
当线段![]() 与图形
与图形![]() 恰有一个公共点时,即
恰有一个公共点时,即![]() 的顶点在线段
的顶点在线段![]() 上,如图2,此时
上,如图2,此时![]() ,
,
∴![]() 的取值范围是:
的取值范围是:![]() .
.



科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进批小型西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该经营户决定降价销售。经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元。该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低多少元?
(1)若设应将每千克的售价降低x元,那么每千克的利润为_____元,降价后何天售出数量为______千克;
(2)请在第(1)小题的基础上,列出方程把此题解答完整。
查看答案和解析>>
科目:初中数学 来源: 题型:
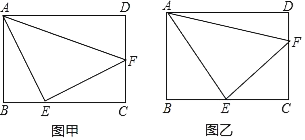
【题目】在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°.如图甲,若EA=EF,则EF=_____;如图乙,若CE=CF,则EF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)为120万元,在销售过程中发现,年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
⑴ 直接写出![]() 关于
关于![]() 的函数关系式为 .
的函数关系式为 .
⑵ 市场管理部门规定,该产品销售单价不得超过100元,该公司销售该种产品当年获利55万元,求当年的销售单价.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+3与x轴交于A,B两点,点A在点B的左侧.
(1)求A,B两点的坐标和此抛物线的对称轴;
(2)设此抛物线的顶点为C,点D与点C关于x轴对称,求四边形ACBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:

小明的作法如下:

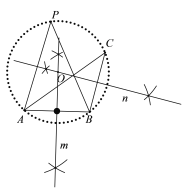
老师说:“小明的作法正确.”
请回答:(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是____;
(2)∠APB=∠ACB的依据是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=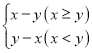 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
(1)请直接写出点(3,5)的“关联点”的坐标 ;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
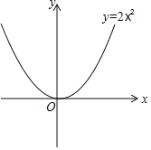
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形,它反映了图形中点的个数与第![]() 个图形之间的某种变化规律.
个图形之间的某种变化规律.
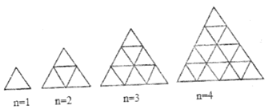
(1)填写下表:
第 | 1 | 2 | 3 | 4 | … |
图形中所有点的个数 | … |
(2)设第![]() 个图形中点的个数是
个图形中点的个数是![]() 个,试写出
个,试写出![]() 与
与![]() 的关系式 .
的关系式 .
(3)若某个图形中所有点的个数是66个,求这是第几个图形?
查看答案和解析>>
科目:初中数学 来源: 题型:
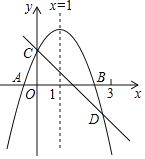
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,则下列结论:
①abc>0
②a﹣b+c<0;
③2a+b+c>0;
④x(ax+b)≤a+b;
其中正确的有_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com