
����Ŀ�����Ͼ�Ӫ����2Ԫ/ǧ�˵ļ۸���С�����ϣ���3Ԫ/ǧ�˵ļ۸���ۣ�ÿ����۳�200ǧ�ˣ�Ϊ�˴������þ�Ӫ�������������ۡ������鷢�֣�����С������ÿ����0.1Ԫ/ǧ�ˣ�ÿ��ɶ��۳�40ǧ��.���⣬ÿ��ķ���ȹ̶��ɱ���24Ԫ���þ�Ӫ��Ҫ��ÿ��ӯ��200Ԫ��Ӧ��ÿǧ��С�����ϵ��ۼ۽��Ͷ���Ԫ?
��1������Ӧ��ÿǧ�˵��ۼ۽���xԪ����ôÿǧ�˵�����Ϊ_____Ԫ�����ۺ�����۳�����Ϊ______ǧ�ˣ�
��2�����ڵ�(1)С��Ļ����ϣ��г����̰Ѵ�����������
���𰸡���1��1-x��200+400x����2��Ӧ��ÿǧ��С�����ϵ��ۼ۽���0.3Ԫ��
��������
��1����������С������ÿ����0.1Ԫ/ǧ�ˣ�ÿ��ɶ��۳�40ǧ�˿�ֱ�ӵó�����ʽ��
��2����Ӧ��ÿǧ��С�����ϵ��ۼ۽���xԪ����ôÿǧ�˵�����Ϊ����3-2-x������������С������ÿ����O.1Ԫ/ǧ�ˣ�ÿ��ɶ��۳�40ǧ�ˣ����Խ���xԪ����ÿ���۳�����Ϊ��200+![]() ǧ�ˣ�
ǧ�ˣ�
����ĵ�����ϵΪ��ÿǧ�˵�������ÿ���۳�����-�̶��ɱ�=200��
��1��
��Ӧ��ÿǧ��С�����ϵ��ۼ۽���xԪ����ôÿǧ�˵�����Ϊ����3-2-x��=(1-x)Ԫ����������С������ÿ����O.1Ԫ/ǧ�ˣ�ÿ��ɶ��۳�40ǧ�ˣ����Խ���xԪ����ÿ���۳�����Ϊ��200+![]() =��200+400x��ǧ��.
=��200+400x��ǧ��.
���1-x �� 200+400x
��2���������⣬�ã�1-x����200+400x��-24=200��
��������̣���x1=0.2��x2=0.3��
��ΪΪ�˴�����x=0.2���������⣬��ȥ��
��x=0.3��
��Ӧ��ÿǧ��С�����ϵ��ۼ۽���0.3Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵʩ�¿γ̸ĸ��ѧϰ��������ϰ���������������кܴ���ߣ�����ʦΪ���˽����̰༶ѧ������ѧϰ�����������ľ���������Ա��ಿ��ѧ��������Ϊ�ڰ���µĸ��ٵ��ˣ��������˽���ֳ����࣬A���ر�ã�B���ã�C��һ�㣻D���ϲ�������˽�����Ƴ�����������������ͳ��ͼ���������ͳ��ͼ�������⣺
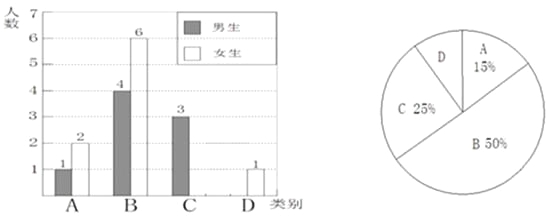
��1�����ε����У�����ʦһ��������������ͬѧ������C��Ů������������D����������������
��2�������������ͳ��ͼ����������
��3��Ϊ�˹�ͬ����������ʦ��ӱ����˵�A���D��ѧ���зֱ�ѡȡһλͬѧ������һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
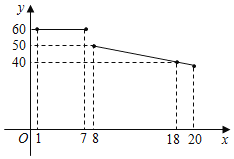
����Ŀ��ijˮ�����о���һ�ֽ���Ϊ18Ԫ/kg��ˮ����������ǰ�����۾��飬����ˮ�������������Ϊ20�죬������Ա����������ˮ�������۵���y��Ԫ/kg�����x�죨1��x��20���ĺ���ͼ����ͼ��ʾ������x�죨1��x��20����������m��kg����x��һ�κ����������±���
x���죩 | 1 | 2 | 3 | �� |
m��kg�� | 20 | 24 | 28 | �� |
��1����ֱ�д�����۵���y��Ԫ/kg����x���죩֮�估������m��kg����x���죩��֮��ĺ�����ϵʽ.
��2���������۵ĵڼ���ʱ����������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
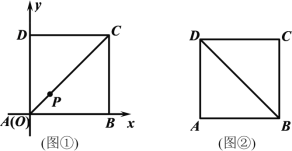
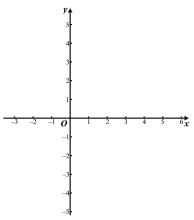
����Ŀ����֪����P�ڱ߳�Ϊ1��������ABCD���ڲ�����P����AD��AB�ľ���ֱ�Ϊm��n.
(1)��AΪԭ�㣬�Ա�AB����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ����ͼ����ʾ������P�ڶԽ���AC�ϣ���m=![]() ʱ�����P�����ꣻ
ʱ�����P�����ꣻ
(2)��ͼ�ڣ���m��n����ʲô����ʱ����P����DAB���ڲ�?��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
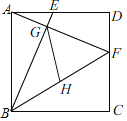
����Ŀ����֪������ABCD�ı߳�Ϊ4����E��F�ֱ���AD��DC�ϣ�AE��DF��1��BE��AF�ཻ�ڵ�G����HΪBF���е㣬����GH����GH�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����������ֱ�ΪA��1��2����B��2��5����C��6��1����������y=![]() �ڵ�һ�����ڵ�ͼ�����ABC�н��㣬��k��ȡֵ��Χ��_____��
�ڵ�һ�����ڵ�ͼ�����ABC�н��㣬��k��ȡֵ��Χ��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��
��![]() ����ͼ���ཻ��A��B���㣨A��B���Ҳࣩ��
����ͼ���ཻ��A��B���㣨A��B���Ҳࣩ��
��1����A��4��2��ʱ�����������Ľ���ʽ��B������ꣻ
��2���ڣ�1���������£�����������ͼ�����һ֧���Ƿ����һ��P��ʹ��PAB����ABΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3����A��a����2a+10����B��b����2b+10��ʱ��ֱ��OA��˷���������ͼ�����һ֧������һ��C������BC��y���ڵ�D����![]() �����ABC�������
�����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijũ���ϰ�������һ���������ó�ABCD���������þ������ó���һ����ȫ����ǽMN��ǽMN�����õij���Ϊ24�ף����������ó���Ϊ50�����Χ�ɣ��������Ҫȫ�����꣬�Ҳ����ǽ�ͷ�IJ��֣�.
(1)��Ҫʹ�������ó������Ϊ300ƽ���ף���ֱ��ǽ��һ�߳�ABΪ�����ף�
(2)�þ������ó�ABCD����������ֵ���������ֵ�������������ʱAB�ij��ȣ���û�����ֵ����˵������.
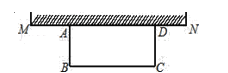
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������������
������������![]() ����ಿ����
����ಿ����![]() �ᷭ�ۣ����ۺ�IJ�������������
�ᷭ�ۣ����ۺ�IJ�������������![]() �ύ���Լ�
�ύ���Լ�![]() ���Ҳಿ�����ͼ��
���Ҳಿ�����ͼ��![]() ����֪
����֪![]()

��1����������![]() �ĶԳ���;
�ĶԳ���;
��2����![]() ʱ��
ʱ��
������![]() ��ͼ��
��ͼ��![]() �ϣ���
�ϣ���![]() ��ֵ;
��ֵ;
��ֱ��д���߶�![]() ��ͼ��
��ͼ��![]() �Ĺ��������;
���������;
��3����n��0ʱ�����߶�![]() ��ͼ��
��ͼ��![]() ǡ�����������㣬ֱ��д��
ǡ�����������㣬ֱ��д��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com