
【题目】已知:一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象相交于A,B两点(A在B的右侧).
)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若![]() ,求△ABC的面积.
,求△ABC的面积.

【答案】(1)![]() ,B(1,8);(2)(﹣4,﹣2)、(﹣16,
,B(1,8);(2)(﹣4,﹣2)、(﹣16,![]() );(3)10.
);(3)10.
【解析】
试题(1)把点A的坐标代入![]() ,就可求出反比例函数的解析式;解一次函数与反比例函数的解析式组成的方程组,就可得到点B的坐标;
,就可求出反比例函数的解析式;解一次函数与反比例函数的解析式组成的方程组,就可得到点B的坐标;
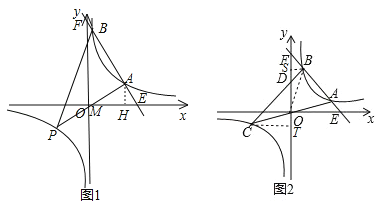
(2)△PAB是以AB为直角边的直角三角形,分两种情况讨论:①若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,求得OE=5,OH=4,AH=2,HE=1.证明△AHM∽△EHA,再根据相似三角形的性质可求出MH,从而得到点M的坐标,然后用待定系数法求出直线AP的解析式,再解直线AP与反比例函数的解析式组成的方程组,就可得到点P的坐标;②若∠ABP=90°,同理即可得到点P的坐标;
(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,易证△CTD∽△BSD,根据相似三角形的性质可得![]() .由A(a,﹣2a+10),B(b,﹣2b+10),可得C(﹣a,2a﹣10),CT=a,BS=b,即可得到
.由A(a,﹣2a+10),B(b,﹣2b+10),可得C(﹣a,2a﹣10),CT=a,BS=b,即可得到![]() .由A、B都在反比例函数的图象上可得a(﹣2a+10)=b(﹣2b+10),把
.由A、B都在反比例函数的图象上可得a(﹣2a+10)=b(﹣2b+10),把![]() 代入即可求出a的值,从而得到点A、B、C的坐标,运用待定系数法求出直线BC的解析式,从而得到点D的坐标及OD的值,然后运用割补法可求出S△COB,再由OA=OC可得S△ABC=2S△COB.
代入即可求出a的值,从而得到点A、B、C的坐标,运用待定系数法求出直线BC的解析式,从而得到点D的坐标及OD的值,然后运用割补法可求出S△COB,再由OA=OC可得S△ABC=2S△COB.
试题解析:(1)把A(4,2)代入![]() ,得k=4×2=8,∴反比例函数的解析式为
,得k=4×2=8,∴反比例函数的解析式为![]() ,解方程组
,解方程组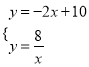 ,得:
,得:![]() 或
或![]() ,∴点B的坐标为(1,8);
,∴点B的坐标为(1,8);
(2)①若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,对于y=﹣2x+10,当y=0时,﹣2x+10=0,解得x=5,∴点E(5,0),OE=5.∵A(4,2),∴OH=4,AH=2,∴HE=5﹣4=1.∵AH⊥OE,∴∠AHM=∠AHE=90°.又∵∠BAP=90°,∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,∴∠MAH=∠AEM,∴△AHM∽△EHA,∴![]() ,∴
,∴![]() ,∴MH=4,∴M(0,0),可设直线AP的解析式为
,∴MH=4,∴M(0,0),可设直线AP的解析式为![]() ,则有
,则有![]() ,解得m=
,解得m=![]() ,∴直线AP的解析式为
,∴直线AP的解析式为![]() ,解方程组
,解方程组 ,得:
,得:![]() 或
或![]() ,∴点P的坐标为(﹣4,﹣2).
,∴点P的坐标为(﹣4,﹣2).
②若∠ABP=90°,同理可得:点P的坐标为(﹣16,![]() ).
).
综上所述:符合条件的点P的坐标为(﹣4,﹣2)、(﹣16,![]() );
);
(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,则有BS∥CT,∴△CTD∽△BSD,∴![]() .∵
.∵![]() ,∴
,∴![]() .∵A(a,﹣2a+10),B(b,﹣2b+10),∴C(﹣a,2a﹣10),CT=a,BS=b,∴
.∵A(a,﹣2a+10),B(b,﹣2b+10),∴C(﹣a,2a﹣10),CT=a,BS=b,∴![]() =
=![]() ,即
,即![]() .∵A(a,﹣2a+10),B(b,﹣2b+10)都在反比例函数
.∵A(a,﹣2a+10),B(b,﹣2b+10)都在反比例函数![]() 的图象上,∴a(﹣2a+10)=b(﹣2b+10),∴a(﹣2a+10)=
的图象上,∴a(﹣2a+10)=b(﹣2b+10),∴a(﹣2a+10)=![]() (﹣2×
(﹣2×![]() +10).∵a≠0,∴﹣2a+10=
+10).∵a≠0,∴﹣2a+10=![]() (﹣2×
(﹣2×![]() +10),解得:a=3.∴A(3,4),B(2,6),C(﹣3,﹣4).
+10),解得:a=3.∴A(3,4),B(2,6),C(﹣3,﹣4).
设直线BC的解析式为![]() ,则有
,则有![]() ,解得:
,解得:![]() ,∴直线BC的解析式为
,∴直线BC的解析式为![]() .当x=0时,y=2,则点D(0,2),OD=2,∴S△COB=S△ODC+S△ODB=
.当x=0时,y=2,则点D(0,2),OD=2,∴S△COB=S△ODC+S△ODB=![]() OD·CT+
OD·CT+![]() OD·BS=
OD·BS=![]() ×2×3+
×2×3+![]() ×2×2=5.∵OA=OC,∴S△AOB=S△COB,∴S△ABC=2S△COB=10.
×2×2=5.∵OA=OC,∴S△AOB=S△COB,∴S△ABC=2S△COB=10.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
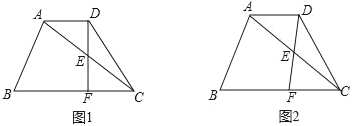
【题目】已知在梯形ABCD中,AD∥BC,AC=BC=10,cos∠ACB=![]() ,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
(1)如图1,当DF⊥BC时,求AD的长;
(2)设EC=y,求y关于x的函数解析式,并直接写出定义域;
(3)当△DFC是等腰三角形时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
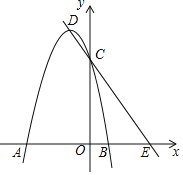
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A,B两点,与y轴相交于点C,顶点为D,直线DC与x轴相交于点E.
(1)当a=﹣1时,求抛物线顶点D的坐标,OE等于多少;
(2)OE的长是否与a值有关,说明你的理由;
(3)设∠DEO=β,45°≤β≤60°,求a的取值范围;
(4)以DE为斜边,在直线DE的左下方作等腰直角三角形PDE.设P(m,n),直接写出n关于m的函数解析式及自变量m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
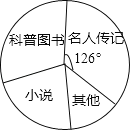
【题目】2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动,200多所学校的师生踊跃参与,向新疆疏勒县中小学共捐赠爱心图书28.5万余本.某学校学生社团对本校九年级学生所捐图书进行统计,根据收集的数据绘制了下面不完整的统计图表.请你根据统计图表中所提供的信息解答下列问题:
图书种类 | 频数(本) | 频率 |
名人传记 | 175 | a |
科普图书 | b | 0.30 |
小说 | 110 | c |
其他 | 65 | d |
(1)求该校九年级共捐书多少本;
(2)统计表中的a= ,b= ,c= ,d= ;
(3)若该校共捐书1500本,请估计“科普图书”和“小说”一共多少本;
(4)该社团3名成员各捐书1本,分别是1本“名人传记”,1本“科普图书”,1本“小说”,要从这3人中任选2人为受赠者写一份自己所捐图书的简介,请用列表法或树状图求选出的2人恰好1人捐“名人传记”,1人捐“科普图书”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校喜迎中华人民共和国成立70周年,将举行以“歌唱祖国”为主题的歌咏比赛,需要在文具店购买国旗图案贴纸和小红旗发给学生做演出道具.已知毎袋贴纸有50张,毎袋小红旗有20面,贴纸和小红旗需整袋购买,每袋贴纸价格比每袋小红旗价格少5元,用150元购买贴纸所得袋数与用200元购买小红旗所得袋数相同.
(1)求每袋国旗图案贴纸和每袋小红旗的价格各是多少元?
(2)如果给每位演出学生分发国旗图案贴纸2张,小红旗1面.设购买国旗图案贴纸![]() 袋(
袋(![]() 为正整数),则购买小红旗多少袋能恰好配套?请用含
为正整数),则购买小红旗多少袋能恰好配套?请用含![]() 的代数式表示.
的代数式表示.
(3)在文具店累计购物超过800元后,超出800元的部分可享受8折优惠.学校按(2)中的配套方案购买,共支付![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?
的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
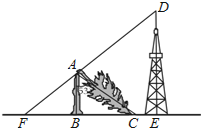
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com