
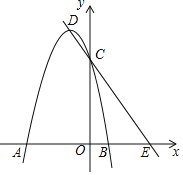
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+2ax��3a��a��0����x���ཻ��A��B���㣬��y���ཻ�ڵ�C������ΪD��ֱ��DC��x���ཻ�ڵ�E��
��1����a=��1ʱ���������߶���D�����꣬OE���ڶ��٣�
��2��OE�ij��Ƿ���aֵ�йأ�˵��������ɣ�
��3�����DEO=�£�45��ܦ¡�60�㣬��a��ȡֵ��Χ��
��4����DEΪб�ߣ���ֱ��DE�����·�������ֱ��������PDE����P��m��n����ֱ��д��n����m�ĺ�������ʽ���Ա���m��ȡֵ��Χ��
���𰸡���1������1��4����3����2�����ۣ�OE�ij���aֵ�أ����ɼ���������3����![]() ��a����1����4��n=��m��1��m��1����
��a����1����4��n=��m��1��m��1����
��������
(1)���ֱ��CD�Ľ���ʽ���ɽ�����⣻
(2)���ò���a�����ֱ��CD�Ľ���ʽ�����E���꼴���жϣ�
(3)����������������µ�a��ֵ�����жϣ�
(4)��ͼ����PM�ͶԳ�����M��PN��AB��N������ȫ�������ε����ʼ��ɽ������.
�⣺(1)��a=��1ʱ�������ߵĽ���ʽΪy=��x2��2x+3��
�ඥ��D(��1��4)��C(0��3)��
��ֱ��CD�Ľ���ʽΪy=��x+3��
��E��3��0����
��OE=3��
(2)���ۣ�OE�ij���aֵ�أ�
���ɣ���y=ax2+2ax��3a��
��C(0����3a)��D(��1����4a)��
��ֱ��CD�Ľ���ʽΪy=ax��3a��
��y=0ʱ��x=3��
��E��3��0����
��OE=3��
��OE�ij���aֵ�أ�
(3)����=45��ʱ��OC=OE=3��
����3a=3��
��a=��1��
����=60��ʱ����Rt��OCE�У�OC=![]() OE=3
OE=3![]() ��
��
����3a=3![]() ��
��
��a=��![]() ��
��
��45��������60�㣬a��ȡֵ��ΧΪ��![]() ��a����1��
��a����1��
(4)��ͼ����PM�ͶԳ�����M��PN��AB��N��

��PD=PE����PMD=��PNE=90�㣬��DPE=��MPN=90�㣬
���DPM=��EPN��
���DPM�ա�EPN��
��PM=PN��PM=EN��
��D(��1����4a)��E(3��0)��
��EN=4+n=3��m��
��n=��m��1��
������D��x����ʱ��P(1����2)����ʱm��ֵ1��
�������ߵĶ����ڵڶ����ޣ�
��m��1��
��n=��m��1(m��1)��
�ʴ�Ϊ��(1)(��1��4)��3��(2)OE�ij���aֵ����(3)��![]() ��a����1��(4)n=��m��1��m��1����
��a����1��(4)n=��m��1��m��1����


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�һ�κ���y=��2x+8��ͼ����x�ᣬy��ֱ��ڵ�A����C������A��AB��x�ᣬ����Ϊ��A������C��CB��y�ᣬ����Ϊ��C�����������ཻ�ڵ�B��

��1���߶�AB��BC��AC�ij��ֱ�ΪAB=�� ����BC=�� ����AC=�� ����
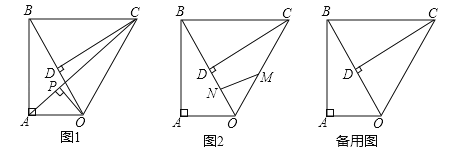
��2���۵�ͼ1�е���ABC��ʹ��A���C�غϣ��ٽ��۵����ͼ��չ�����ۺ�DE��AB�ڵ�D����AC�ڵ�E������CD����ͼ2��
�������A��B��������ѡһ��������ѡ���� ���⣮
A�������߶�AD�ij���
����y���ϣ��Ƿ���ڵ�P��ʹ����APDΪ���������Σ������ڣ���ֱ��д���������������е�P�����ꣻ�������ڣ���˵�����ɣ�
B�������߶�DE�ij���
��������ƽ���ڣ��Ƿ���ڵ�P������B�⣩��ʹ���Ե�A��P��CΪ���������������ABCȫ�ȣ������ڣ���ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ������Ϊ4Ԫ������Ʒ������ÿ��5Ԫ�ļ۸����ۣ�ÿ��������3���������ÿ��6Ԫ�ļ۸����ۣ�ÿ��������2������ٶ�ÿ�����ۼ���y��������۸�x��Ԫ/����֮������һ�κ�����ϵ��
��1������y��x֮��ĺ�����ϵʽ��
��2�������ۼ۸�Ϊ����ʱ������ʹÿ�µ��������ÿ�µ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��
��![]() ���
���![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ����ͼ1������
����ͼ1������![]() ��
��
��1����գ�![]() ����
����![]() ��
��
��2����ͼ1������![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() �ij��ȣ�
�ij��ȣ�
��3����ͼ2����![]() ��
��![]() ͬʱ�ӵ�
ͬʱ�ӵ�![]() ��������
��������![]() �����˶���
�����˶���![]() ��
��![]() ·�������˶���
·�������˶���![]() ��
��![]() ·�������˶�������������ʱ�˶�ֹͣ����֪��
·�������˶�������������ʱ�˶�ֹͣ����֪��![]() ���˶��ٶ�Ϊ1.5��λ
���˶��ٶ�Ϊ1.5��λ![]() �룬��
�룬��![]() ���˶��ٶ�Ϊ1��λ
���˶��ٶ�Ϊ1��λ![]() �룬���˶�ʱ��Ϊ
�룬���˶�ʱ��Ϊ![]() �룬
�룬![]() �����Ϊ
�����Ϊ![]() ����
����![]() Ϊ��ֵʱ
Ϊ��ֵʱ![]() ȡ�����ֵ�����ֵΪ���٣�
ȡ�����ֵ�����ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
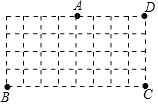
����Ŀ����ͼ���ɱ߳�Ϊ1��С��������ɵ�8��4����ÿ��С�����εĶ��������㣬��A��B��C��D���ڸ���ϣ��������н���D�����в����ƶ���
��һ������D�Ƶ�A˳ʱ����ת180��õ���D1��
�ڶ�������D1�Ƶ�B˳ʱ����ת90��õ���D2��
����������D2�Ƶ�C˳ʱ����ת90��ص���D��
��1������Բ�滭����D��D1��D2��D������·����
��2������ͼ����ʲô�Գ�ͼ�Σ�
��3��������ͼ�ε��ܳ�����������У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y��ax2+bx+c����A����3��0����B����2��3����C��0��3��������ΪD��
��1���������ߵĽ���ʽ��
��2�����M��1��m������MB+MD��ֵ��Сʱ����m��ֵ��
��3����P����������λ��ֱ��AC�Ϸ���һ�����㣬���APC����������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
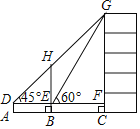
����Ŀ����ͼ��ij��ѧ��ȤС��Ϊ����һ�ù���BH�ͽ�ѧ¥CG�ĸߣ�����A���ø�1.5�IJ���Dz�ù�������H�����ǡ�HDEΪ45�㣬��ʱ��ѧ¥����Gǡ��������DH�ϣ�����ǰ��7����B�����ֲ�ý�ѧ¥����G�����ǡ�GEFΪ60�㣬��A��B��C������ͬһˮƽ���ϣ�
��1���������BH�ĸߣ�
��2�������ѧ¥CG�ĸߣ����ο����ݣ�![]() ��14��
��14��![]() ��1.7��
��1.7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2-4x+c(a��0)�뷴��������y=![]() ��ͼ���ཻ��B�㣬��B��ĺ�����Ϊ3����������y�ύ�ڵ�C(0,6)��A��������y=ax2-4x+c�Ķ��㣬P����x����һ���㣬��PA+PB��Сʱ��P�������Ϊ_______��
��ͼ���ཻ��B�㣬��B��ĺ�����Ϊ3����������y�ύ�ڵ�C(0,6)��A��������y=ax2-4x+c�Ķ��㣬P����x����һ���㣬��PA+PB��Сʱ��P�������Ϊ_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣����꼶��ѧ��ȤС�龭���г����飬�õ�ij���˶���ÿ�µ��������ۼ۵������Ϣ���±���
�ۼۣ�Ԫ/���� | 100 | 110 | 120 | 130 | �� |
������������ | 200 | 180 | 160 | 140 | �� |
��֪���˶����Ľ���Ϊÿ��60Ԫ�����ۼ�Ϊ![]() Ԫ��
Ԫ��
��1�����ú�x��ʽ�ӱ�ʾ�������۸��˶���ÿ���������� Ԫ������������ ������ֱ��д�������
��2�������۸��˶�����������Ϊ![]() Ԫ����ô�ۼ�Ϊ����ʱ�����µ����������������Ƕ��٣�
Ԫ����ô�ۼ�Ϊ����ʱ�����µ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com