
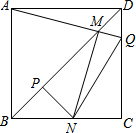
 边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,有下列结论:
边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,有下列结论:分析 由题可知A,B,N,M四点共圆,进而可得出∠ANM=∠NAM=45°,由等角对等边知,AM=MN,故①正确;
由同角的余角相等知,∠HAM=∠PMN,所以Rt△AHM≌Rt△MPN,即可得出结论,故②正确;
因为∠BAN+∠QAD=∠NAQ=45°,在∠NAM作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,所以△ABN≌△UAN,△DAQ≌△UAQ,有∠UAN=∠UAQ=90°,BN=NU,DQ=UQ,即可得出结论,故③正确;
先由题意得出四边形SMWB是正方形,进而证出△AMS≌△NMW,因为AS=NW,所以AB+BN=SB+BW=2BW,而BW:BM=1:$\sqrt{2}$,即可求出$\frac{AB+BN}{BM}$=$\sqrt{2}$,故④正确.
解答 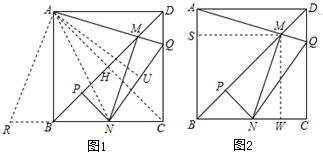 (1)解:①②③④;
(1)解:①②③④;
(2)证明:①如图1,作AU⊥NQ于U,交BD于H,连接AN,AC,
∵∠AMN=∠ABC=90°,
∴A,B,N,M四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴AM=MN;
②由同角的余角相等知,∠HAM=∠PMN,
∴Rt△AHM≌Rt△MPN,
∴MP=AH=$\frac{1}{2}$AC=$\frac{1}{2}$BD;
③∵∠BAN+∠QAD=∠NAQ=45°,
∴在∠NAM作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,
∴△ABN≌△UAN,△DAQ≌△UAQ,有∠UAN=∠UAQ,BN=NU,DQ=UQ,
∴点U在NQ上,有BN+DQ=QU+UN=NQ;
④如图2,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,
∴四边形SMWB是正方形,有MS=MW=BS=BW,
∴△AMS≌△NMW
∴AS=NW,
∴AB+BN=SB+BW=2BW,
∵BW:BM=1:$\sqrt{2}$,
∴$\frac{AB+BN}{BM}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$.
点评 本题考查了正方形的性质,四点共圆的判定,圆周角定理,等腰直角三角形的性质,全等三角形的判定和性质等知识,正确作出辅助线并运用有关知识理清图形中线段间的关系是解答本题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
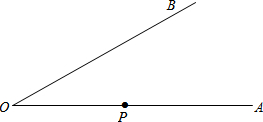 如图所示,已知∠AOB,点P在OA上.
如图所示,已知∠AOB,点P在OA上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
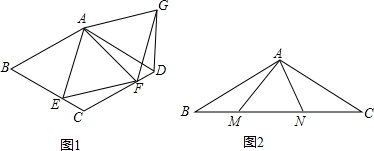
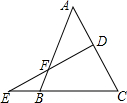 如图所示,已知D为△ABC的边AC上的一点,E为CB的延长线上的一点,且$\frac{EF}{FD}$=$\frac{AC}{BC}$.求证:AD=EB.
如图所示,已知D为△ABC的边AC上的一点,E为CB的延长线上的一点,且$\frac{EF}{FD}$=$\frac{AC}{BC}$.求证:AD=EB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
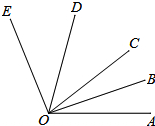 如图,∠AOE=100°,射线OD、OB是∠EOC、∠COA的角平分线.
如图,∠AOE=100°,射线OD、OB是∠EOC、∠COA的角平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com