
【题目】阅读下列材料,并按要求解答.
(模型建立)如图①,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA.
(模型应用)
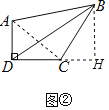
应用1:如图②,在四边形ABCD中,∠ADC=90°,AD=6,CD=8,BC=10,AB2=200.求线段BD的长.
应用2:如图 ③,在平面直角坐标系中,纸片△OPQ为等腰直角三角形,QO=QP,P(4,m),点Q始终在直线OP的上方.
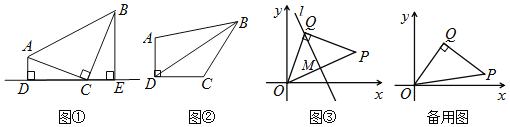
(1)折叠纸片,使得点P与点O重合,折痕所在的直线l过点Q且与线段OP交于点M,当m=2时,求Q点的坐标和直线l与x轴的交点坐标;
(2)若无论m取何值,点Q总在某条确定的直线上,请直接写出这条直线的解析式 .
【答案】模型建立:见解析;应用1:2![]() ;应用2:(1)Q(1,3),交点坐标为(
;应用2:(1)Q(1,3),交点坐标为(![]() ,0);(2)y=﹣x+4
,0);(2)y=﹣x+4
【解析】
根据AAS证明△BEC≌△CDA,即可;
应用1:连接AC,过点B作BH⊥DC,交DC的延长线于点H,易证△ADC≌△CHB,结合勾股定理,即可求解;
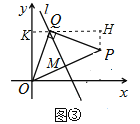
应用2:(1)过点P作PN⊥x轴于点N,过点Q作QK⊥y轴于点K,直线KQ和直线NP相交于点H,易得:△OKQ≌△QHP,设H(4,y),列出方程,求出y的值,进而求出Q(1,3),再根据中点坐标公式,得P(4,2),即可得到直线l的函数解析式,进而求出直线l与x轴的交点坐标;(2)设Q(x,y),由△OKQ≌△QHP,KQ=x,OK=HQ=y,可得:y=﹣x+4,进而即可得到结论.
如图①,∵AD⊥ED,BE⊥ED,∠ACB=90°,
∴∠ADC=∠BEC=90°,
∴∠ACD+∠DAC=∠ACD+∠BCE=90°,
∴∠DAC=∠BCE,
∵AC=BC,
∴△BEC≌△CDA(AAS);
应用1:如图②,连接AC,过点B作BH⊥DC,交DC的延长线于点H,
∵∠ADC=90°,AD=6,CD=8,
∴AC=10,
∵BC=10,AB2=200,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∵∠ADC=∠BHC=∠ACB=90°,
∴∠ACD=∠CBH,
∵AC=BC=10,
∴△ADC≌△CHB(AAS),
∴CH=AD=6,BH=CD=8,
∴DH=6+8=14,
∵BH⊥DC,
∴BD=![]() =2
=2![]() ;
;
应用2:(1)如图③,过点P作PN⊥x轴于点N,过点Q作QK⊥y轴于点K,直线KQ和直线NP相交于点H,
由题意易:△OKQ≌△QHP(AAS),
设H(4,y),那么KQ=PH=y﹣m=y﹣2,OK=QH=4﹣KQ=6﹣y,
又∵OK=y,
∴6﹣y=y,y=3,
∴Q(1,3),
∵折叠纸片,使得点P与点O重合,折痕所在的直线l过点Q且与线段OP交于点M,
∴点M是OP的中点,
∵P(4,2),
∴M(2,1),
设直线Q M的函数表达式为:y=kx+b,
把Q(1,3),M(2,1),代入上式得:![]() ,解得:
,解得:![]()
∴直线l的函数表达式为:y=﹣2x+5,
∴该直线l与x轴的交点坐标为(![]() ,0);
,0);
(2)∵△OKQ≌△QHP,
∴QK=PH,OK=HQ,
设Q(x,y),
∴KQ=x,OK=HQ=y,
∴x+y=KQ+HQ=4,
∴y=﹣x+4,
∴无论m取何值,点Q总在某条确定的直线上,这条直线的解析式为:y=﹣x+4,
故答案为:y=﹣x+4.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
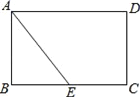
【题目】如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是______ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 y=a(x﹣2)![]() +1 经过点 P(1,﹣3)
+1 经过点 P(1,﹣3)
(1)求 a 的值;
(2)若点 A(m,y![]() )、B(n ,y
)、B(n ,y![]() )(m<n<2)都在该抛物线上,试比较 y
)(m<n<2)都在该抛物线上,试比较 y![]() 与y
与y![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对“安全常识”的掌握程度,随机抽取部分学生安全知识竞赛的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.图中A表示“不了解”,B表示“了解很少”、C表示“基本了解”,D表示“非常了解”.请根据统计图所提供的信息解答下列问题:
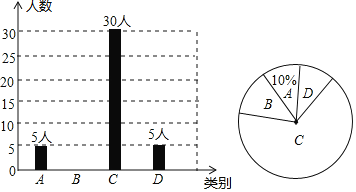
(1)被调查的总人数是 人,扇形统计图中A部分所对应的扇形圆心角的度数为 度;
(2)补全条形统计图;
(3)若该校共有学生1500人,请根据上述调查结果,估计该校学生中达到“基本了解”和“非常了解”共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况.请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年4月20日,四川雅安发生里氏7.0级地震,救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距4米,探测线与地面的夹角分别为300和600,如图所示,试确定生命所在点C的深度(结果精确到0.1米,参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
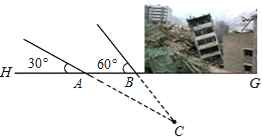
查看答案和解析>>
科目:初中数学 来源: 题型:
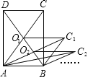
【题目】如图,矩形![]() 的面积为
的面积为![]() ,它的两条对角线交于点
,它的两条对角线交于点![]() ,以
,以![]() 、
、![]() 为两邻边作平行四边形
为两邻边作平行四边形![]() ,平行四边形
,平行四边形![]() 的对角线交于点
的对角线交于点![]() ,同样以
,同样以![]() 、
、![]() 为两邻边作平行四边形
为两邻边作平行四边形![]() ,…,依此类推,则平行四边形
,…,依此类推,则平行四边形![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
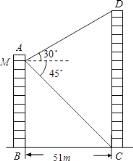
【题目】如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.(![]() 取1.73,结果保留整数)
取1.73,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中,装有红、黄、白、黑四种只有颜色不同的小球,其中红色小球有30个,黄、白、黑色小球的数目相同.为估计袋中黄色小球的数目,每次将袋中小球搅匀后摸出一个小球记下颜色,放回后再次搅匀…多次试验发现摸到红球的频率是![]() ,则估计黄色小球的数目是 .
,则估计黄色小球的数目是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com