
 小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长2$\sqrt{3}$,钓竿AO的倾斜角∠ODC是60°,其长OA为5米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长2$\sqrt{3}$,钓竿AO的倾斜角∠ODC是60°,其长OA为5米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离. 分析 先根据三角形内角和定理求出∠CAD=180°-∠ODB-∠ACD=90°,解Rt△ACD,得出AD=AC•tan∠ACD=2米,CD=2AD=3米,再证明△BOD是等边三角形,得到BD=OD=OA+AD=7米,然后根据BC=BD-CD即可求出浮漂B与河堤下端C之间的距离.
解答 解:∵AO的倾斜角是60°,
∴∠ODB=60°.
∵∠ACD=30°,
∴∠CAD=180°-∠ODB-∠ACD=90°.
在Rt△ACD中,AD=AC•tan∠ACD=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2(米),
∴CD=2AD=4米,
又∵∠O=60°,
∴△BOD是等边三角形,
∴BD=OD=OA+AD=2+5=7(米),
∴BC=BD-CD=7-4=3(米).
答:浮漂B与河堤下端C之间的距离为3米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据所给的倾斜角构造直角三角形,利用三角函数的知识求解.


科目:初中数学 来源: 题型:解答题
 已知,如图,△ABC和△DBE均为等腰直角三角形,其中∠ABC=90°,∠DBE=90°.
已知,如图,△ABC和△DBE均为等腰直角三角形,其中∠ABC=90°,∠DBE=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
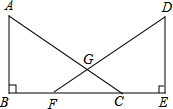 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2-x-6分解因式.这个式子的常数项-6=2×(-3),一次项系数-1=2+(-3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.
阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2-x-6分解因式.这个式子的常数项-6=2×(-3),一次项系数-1=2+(-3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价 x(元) | 16 | 18 | 20 | 22 |
| 年销售量y(万件) | 5 | 4 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com