
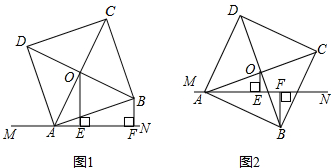
分析 (1)过点B作BG⊥OE于G,推出四边形BGEF是矩形,根据矩形的性质得出EF=BG,BF=GE,求出OA=OB,∠OBG+∠BOE=90°,∠AOE=∠OBG,根据AAS推出△AOE≌△OBG,根据全等得出OG=AE,OE=BG即可;
(2)过点B作BG⊥OE交OE的延长线于G,推出四边形BGEF是矩形,根据矩形的性质得出EF=BG,BF=GE,求出OA=OB,∠OBG+∠BOE=90°,∠AOE=∠OBG,根据AAS推出△AOE≌△OBG,根据全等三角形的性质得出OG=AE,OE=BG即可.
解答 (1)证明:如图1,过点B作BG⊥OE于G,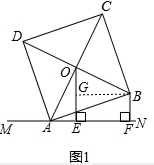
则四边形BGEF是矩形,
所以EF=BG,BF=GE,
在正方形ABCD中,OA=OB,∠AOB=90°,
∵BG⊥OE,
∴∠OBG+∠BOE=90°,
又∵∠AOE+∠BOE=90°,
∴∠AOE=∠OBG,
∵在△AOE和△OBG中,
$\left\{\begin{array}{l}{∠AOE=∠OBG}\\{∠AEO=∠OGB}\\{OA=OB}\end{array}\right.$
∴△AOE≌△OBG(AAS),
∴OG=AE,OE=BG,
∵AF=AE+EF,
又∵OE=BG,EF=BG
∴AF=AE+OE;
(2)解:图2结论:AF=AE+OE,
理由是:如图2,过点B作BG⊥OE交OE的延长线于G,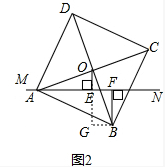
则四边形BGEF是矩形,
所以EF=BG,BF=GE,
在正方形ABCD中,OA=OB,∠AOB=90°,
∵BG⊥OE,
∴∠OBG+∠BOE=90°,
又∵∠AOE+∠BOE=90°,
∴∠AOE=∠OBG,
∵在△AOE和△OBG中,
$\left\{\begin{array}{l}{∠AOE=∠OBG}\\{∠AEO=∠OGB}\\{OA=OB}\end{array}\right.$
∴△AOE≌△OBG(AAS),
∴OG=AE,OE=BG,
∵AF=AE+EF,
又∵OE=BG,EF=BG
∴AF=AE+OE.
点评 本题考查了矩形的性质和判定,正方形的性质,三角形的内角和定理,全等三角形的性质和判定的应用,解此题的关键是能正确作出辅助线,并进一步推出△AOE≌△OBG,证明过程类似.


科目:初中数学 来源: 题型:解答题
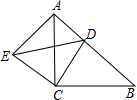 如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.
如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 购买一张彩票,中奖 | |
| B. | 一个袋中只装有2个黑球,从中摸出一个球是黑球 | |
| C. | 抛掷一枚硬币,正面向上 | |
| D. | 打开电视,正在播放广告 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩 | 频数 | 百分比 |
| 不及格 | a | m |
| 及格 | 14 | 20% |
| 良好 | b | 40% |
| 优秀 | 21 | 30% |
| 合计 | 70 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是某班对40名学生上学出行方式调查的扇形统计图,问:
如图是某班对40名学生上学出行方式调查的扇形统计图,问:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 没有水分,种子发芽 | B. | 367人中至少有2人的生日相同 | ||
| C. | 三角形的内角和是180° | D. | 小华一出门上学,天就下雨 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com