
【题目】若关于![]() 的不等式组
的不等式组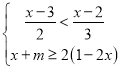 有且仅有三个整数解,且关于
有且仅有三个整数解,且关于![]() 的分式方程
的分式方程![]() 的解为整数,则符合条件的整数
的解为整数,则符合条件的整数![]() 的个数是
的个数是![]()
![]()
A. 1个B. 2个C. 3个D. 4个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
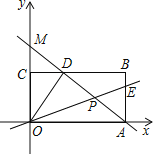
【题目】如图,已知长方形OABC的顶点O在坐标原点,A、C分别在x、y轴的正半轴上,顶点B(8,6),直线y=-x+b经过点A交BC于D、交y轴于点M,点P是AD的中点,直线OP交AB于点E
(1)求点D的坐标及直线OP的解析式;
(2)求△ODP的面积,并在直线AD上找一点N,使△AEN的面积等于△ODP的面积,请求出点N的坐标
(3)在x轴上有一点T(t,0)(5<t<8),过点T作x轴的垂线,分别交直线OE、AD于点F、G,在线段AE上是否存在一点Q,使得△FGQ为等腰直角三角形,若存在,请求出点Q的坐标及相应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
![]()
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①②B. ①③C. ①②③D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于
与x轴交于![]() 两点,直线
两点,直线![]() 与y 轴交于点
与y 轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() 。
。
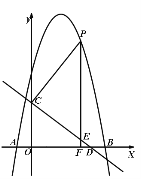
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点、是否存在点
的对称点、是否存在点![]() ,使点
,使点![]() 落在y轴上?若存在,求出相应的点
落在y轴上?若存在,求出相应的点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
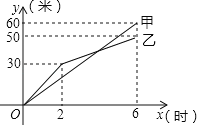
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=﹣![]() x2+bx+c的图象经过A、E两点,且点E的坐标为(﹣
x2+bx+c的图象经过A、E两点,且点E的坐标为(﹣![]() ,0),以0C为直径作半圆,圆心为D.
,0),以0C为直径作半圆,圆心为D.
(1)求二次函数的解析式;
(2)求证:直线BE是⊙D的切线;
(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.
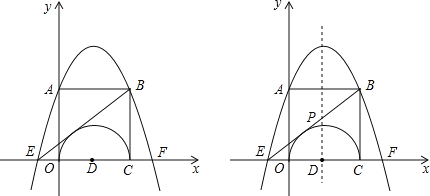
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com