
【题目】如图,抛物线![]() 与x轴交于
与x轴交于![]() 两点,直线
两点,直线![]() 与y 轴交于点
与y 轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() 。
。
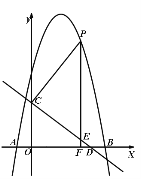
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点、是否存在点
的对称点、是否存在点![]() ,使点
,使点![]() 落在y轴上?若存在,求出相应的点
落在y轴上?若存在,求出相应的点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
【答案】(1)y=-x2+4x+5.(2) m=2或m=![]() .(3) 点P坐标为(-
.(3) 点P坐标为(-![]() ,
,![]() ),(4,5),(3-
),(4,5),(3-![]() ,2
,2![]() -3).
-3).
【解析】
试题(1)利用待定系数法求出抛物线的解析式;
(2)用含m的代数式分别表示出PE、EF,然后列方程求解;
(3)解题关键是识别出当四边形PECE′是菱形,然后根据PE=CE的条件,列出方程求解;当四边形PECE′是菱形不存在时,P点y轴上,即可得到点P坐标.
试题解析:(1)将点A、B坐标代入抛物线解析式,得:
![]() ,
,
解得![]() ,
,
∴抛物线的解析式为:y=-x2+4x+5.
(2)∵点P的横坐标为m,
∴P(m,-m2+4m+5),E(m,-![]() m+3),F(m,0).
m+3),F(m,0).
∴PE=|yP-yE|=|(-m2+4m+5)-(-![]() m+3)|=|-m2+
m+3)|=|-m2+![]() m+2|,
m+2|,
EF=|yE-yF|=|(-![]() m+3)-0|=|-
m+3)-0|=|-![]() m+3|.
m+3|.
由题意,PE=5EF,即:|-m2+![]() m+2|=5|-
m+2|=5|-![]() m+3|=|-
m+3|=|-![]() m+15|
m+15|
①若-m2+![]() m+2=-
m+2=-![]() m+15,整理得:2m2-17m+26=0,
m+15,整理得:2m2-17m+26=0,
解得:m=2或m=![]() ;
;
②若-m2+![]() m+2=-(-
m+2=-(-![]() m+15),整理得:m2-m-17=0,
m+15),整理得:m2-m-17=0,
解得:m=![]() 或m=
或m=![]() .
.
由题意,m的取值范围为:0<m<5,故m=![]() 、m=
、m=![]() 这两个解均舍去.
这两个解均舍去.
∴m=2或m=![]() .
.
(3)假设存在.
作出示意图如下:
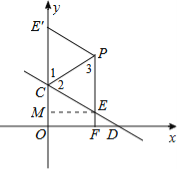
∵点E、E′关于直线PC对称,
∴∠1=∠2,CE=CE′,PE=PE′.
∵PE平行于y轴,∴∠1=∠3,
∴∠2=∠3,∴PE=CE,
∴PE=CE=PE′=CE′,即四边形PECE′是菱形.
当四边形PECE′是菱形存在时,
由直线CD解析式y=-![]() x+3,可得OD=4,OC=3,由勾股定理得CD=5.
x+3,可得OD=4,OC=3,由勾股定理得CD=5.
过点E作EM∥x轴,交y轴于点M,易得△CEM∽△CDO,
∴![]() ,
,
即![]() ,
,
解得CE=![]() |m|,
|m|,
∴PE=CE=![]() |m|,
|m|,
又由(2)可知:PE=|-m2+![]() m+2|
m+2|
∴|-m2+![]() m+2|=
m+2|=![]() |m|.
|m|.
①若-m2+![]() m+2=
m+2=![]() m,整理得:2m2-7m-4=0,
m,整理得:2m2-7m-4=0,
解得m=4或m=-![]() ;
;
②若-m2+![]() m+2=-
m+2=-![]() m,整理得:m2-6m-2=0,解得m1=3+
m,整理得:m2-6m-2=0,解得m1=3+![]() ,m2=3-
,m2=3-![]() .
.
由题意,m的取值范围为:-1<m<5,故m=3+![]() 这个解舍去.
这个解舍去.
当四边形PECE′是菱形这一条件不存在时,
此时P点横坐标为0,E,C,E'三点重合与y轴上,菱形不存在,即P点为(0,5).
综上所述,存在满足条件的点P,可求得点P坐标为(-![]() ,
,![]() ),(4,5),(3-
),(4,5),(3-![]() ,2
,2![]() -3)
-3)


科目:初中数学 来源: 题型:
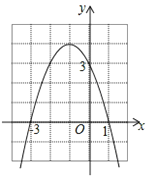
【题目】如图所示是二次函数y=ax2+bx+c的图象.下列结论:①二次三项式ax2+bx+c的最大值为4;②使y≤3成立的x的取值范围是x≤-2;③一元二次方程ax2+bx+c=1的两根之和为-1;④该抛物线的对称轴是直线x=-1;⑤4a-2b+c<0.其中正确的结论有______________.(把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
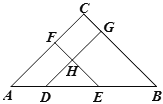
【题目】如图,在△ABC中 ,∠A=∠B,D、E是边AB上的点,DG∥AC,EF∥BC,DG、EF相 交于点H.
(1)∠HDE与∠HED是否相等?并说明理由.
解:∠HDE=∠HED.理由如下:
∵DG∥AC(已知)
∴ = ( )
∵ EF∥BC (已知)
∴ = ( )
又∵∠A=∠B (已知)
∴ = ( ).
(2)如果∠C=90°,DG、 EF有何位置关系?并仿照 (1)中的解答方法说明理由.
解: .理由如下:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车专卖店销售某种型号的汽车.已知该型号汽车的进价为10万元/辆,销售一段时间后发现:当该型号汽车售价定为15万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出2辆.
(1)若要平均每周售出汽车不低于15辆,该汽车的售价最多定为多少万元?
(2)该店计划下调售价,尽可能增加销量,减少库存,但要确保平均每周的销售利润为40万元,每辆汽车的售价定为多少合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校学生会组织了一次全校1200名学生参加的“汉字听写”大赛,并设成绩优胜奖.
赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中100名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.10 |
60≤x<70 | 25 | 0.25 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.20 |
90≤x≤100 | 15 | 0.15 |
成绩在70≤x<80这一组的是:
70 70 71 71 71 72 72 73 73 73 73 75 75 75 75 76 76 76 76 76 76 76 76 77 77 78 78 78 79 79
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数是 ;
(4)若这次比赛成绩在78分以上(含78分)的学生获得优胜奖,则该校参加这次比赛的1200名学生中获优胜奖的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD为矩形,点O是AC的中点,过点O的一直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO,若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB:OE=3:2,其中正确结论是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com