
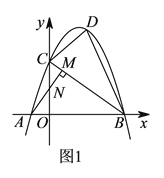
【题目】如图1,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点, ![]() 于点
于点![]() 交
交![]() 轴于点
轴于点![]() .已知抛物线
.已知抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() .
.
(![]() )求抛物线的函数式.
)求抛物线的函数式.
(![]() )连接
)连接![]() ,点
,点![]() 在线段
在线段![]() 上方的抛物线上,连接
上方的抛物线上,连接![]() 、
、![]() ,若
,若![]() 和
和![]() 面积满足
面积满足![]() ,求点
,求点![]() 的坐标.
的坐标.
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 中点,设
中点,设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() .一动点
.一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() ,再沿着线段
,再沿着线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止.若点
后停止.若点![]() 在整个运动过程中用时最少,请直接写出最少时间和此时点
在整个运动过程中用时最少,请直接写出最少时间和此时点![]() 的坐标.
的坐标.
【答案】(1)抛物线解析式为![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() 或
或![]() ;(3)此时
;(3)此时![]() ,
, ![]() .
.
【解析】试题分析:(1)先证明△AON∽△COB,利用相似比计算出OA=1,得到A(-1,0),然后利用交点式可求出抛物线解析式为y=-![]() x2+
x2+![]() x+3;
x+3;
(2)先利用待定系数法求出直线BC的解析式为y=-![]() x+3,作PQ∥y轴交BC于Q,如图1,设P(x,-
x+3,作PQ∥y轴交BC于Q,如图1,设P(x,-![]() x2+
x2+![]() x+3),则Q(x,-
x+3),则Q(x,-![]() x+3),再计算出DQ=-
x+3),再计算出DQ=-![]() x2+3x,根据三角形面积公式得S△BCD=S△CDQ+S△BDQ=-
x2+3x,根据三角形面积公式得S△BCD=S△CDQ+S△BDQ=-![]() x2+6x,然后根据S△BCD=
x2+6x,然后根据S△BCD=![]() S△ABC得到-
S△ABC得到-![]() x2+6x=
x2+6x=![]() ×
×![]() ×(4+1)×3,然后解方程求出x即可得到D点坐标;
×(4+1)×3,然后解方程求出x即可得到D点坐标;
(3)过![]() 做
做![]() 平行
平行![]() 轴交抛物线于
轴交抛物线于![]() ,过
,过![]() 做
做![]() ,可证
,可证![]() ,由此
,由此![]() ,过
,过![]() 作
作![]() 的垂线,交点即为
的垂线,交点即为![]() 点,可得
点,可得![]() 值和点
值和点![]() 坐标.
坐标.
试题解析:( ![]() )
)![]() ,
,
![]() ,
,
∴![]() ,
,
且![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() .
.
设抛物线解析式为![]() ,
,
将![]() 代入得
代入得![]() ,
,
∴抛物线解析式为![]() .
.
(![]() )设直线
)设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() ,
, ![]() 代入得
代入得![]() ,
,
解得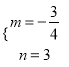 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
作![]() 轴交
轴交![]() 于
于![]() ,如图1,设
,如图1,设
![]() ,则
,则![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
整理得![]() ,解得
,解得![]() ,
, ![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
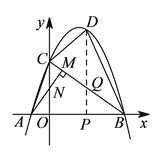
(![]() )设运动时间为
)设运动时间为![]() ,则
,则
![]() ,
,
![]() ,
,
过![]() 做
做![]() 平行
平行![]() 轴交抛物线于
轴交抛物线于![]() ,过
,过![]() 做
做![]() ,
,
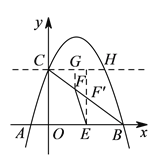
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
过![]() 作
作![]() 的垂线,交点即为
的垂线,交点即为![]() 点,
点,
此时![]() ,
,
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】清明期间,某校师生组成200个小组参加“保护环境,美化家园”植树活动.综合实际情况,校方要求每小组植树量为2至5棵,活动结束后,校方随机抽查了其中50个小组,根据他们的植树量绘制出如图所示的两幅不完整统计图.请根据图中提供的信息,解答下面的问题:

(1)请把条形统计图补充完整,并算出扇形统计图中,植树量为“5棵树”的圆心角是 °.
(2)请你帮学校估算此次活动共种多少棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,点A、C分别在y轴和x轴上,AB∥x轴,cosB=![]() .点P从B点出发,以1cm/s的速度沿边BA匀速运动,点Q从点A出发,沿线段AO-OC-CB匀速运动.点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△BPQ的面积为S(cm2), 已知S与t之间的函数关系如图(2)中的曲线段OE、线段EF与曲线段FG.
.点P从B点出发,以1cm/s的速度沿边BA匀速运动,点Q从点A出发,沿线段AO-OC-CB匀速运动.点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△BPQ的面积为S(cm2), 已知S与t之间的函数关系如图(2)中的曲线段OE、线段EF与曲线段FG.
(1)点Q的运动速度为 cm/s,点B的坐标为 ;
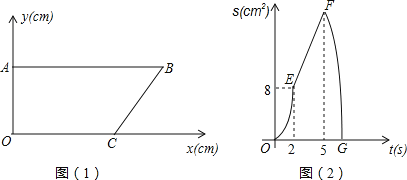
(2)求曲线FG段的函数解析式;
(3)当t为何值时,△BPQ的面积是四边形OABC的面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
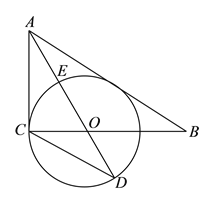
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的角平分线,以
的角平分线,以![]() 为圆心,
为圆心, ![]() 为半径作⊙
为半径作⊙![]() .
.
(![]() )求证:
)求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )已知
)已知![]() 交⊙
交⊙![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() ,
, ![]() ,求
,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的条件下,设⊙
)的条件下,设⊙![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列能判定两个三角形全等的是( )
①三条边对应相等;②三个角对应相等;③两边和一个角对应相等;④两角和它们的夹边对应相等;⑤两角和一个角的对边对应相等.
A. ①②③ B. ①③⑤ C. ②③④ D. ①④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com