
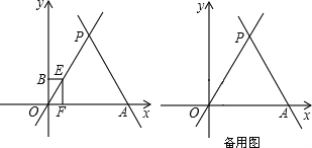
【题目】如图,直线![]() 与x轴相交于点A,与直线
与x轴相交于点A,与直线![]() 相交于点P.
相交于点P.
(1)求点P的坐标.
(2)请判断△OPA的形状并说明理由.
(3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.求S与t之间的函数关系式.
【答案】(1)![]() ;(2)△POA是等边三角形,理由见解析;(3)当0<t≤4时,
;(2)△POA是等边三角形,理由见解析;(3)当0<t≤4时,![]() ,当4<t<8时,
,当4<t<8时,![]()
【解析】
(1)将两直线的解析式联立组成方程组,解得x、y的值即为两直线的交点坐标的横纵坐标;
(2)求得直线AP与x轴的交点坐标(4,0),利用OP=4PA=4得到OA=OP=PA从而判定△POA是等边三角形;
(3)分别求得OF和EF的值,利用三角形的面积计算方法表示出三角形的面积即可.
解:(1)解方程组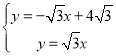 ,
,
解得: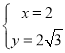 .
.
∴点P的坐标为:![]() ;
;
(2)当y=0时,x=4,
∴点A的坐标为(4,0).
∵![]() ,
,
∴OA=OP=PA,
∴△POA是等边三角形;
(3)①当0<t≤4时,如图,在Rt△EOF中,
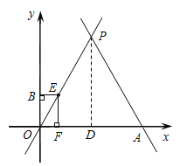
∵∠EOF=60°,OE=t,
∴EF=![]() ,OF=
,OF=![]() ,
,
∴![]() .
.
当4<t<8时,如图,设EB与OP相交于点C,
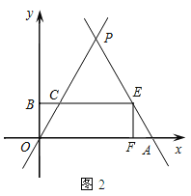
∵CE=PE=t-4,AE=8-t,
∴AF=4-![]() ,EF=
,EF=![]() ,
,
∴OF=OA-AF=4-(4-![]() )=
)=![]() ,
,
∴![]()
=![]() ;
;
综合上述,可得:当0<t≤4时,![]() ;当4<t<8时,
;当4<t<8时,![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
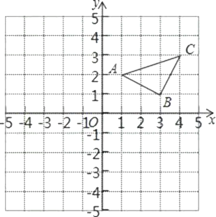
【题目】已知:如图所示.
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
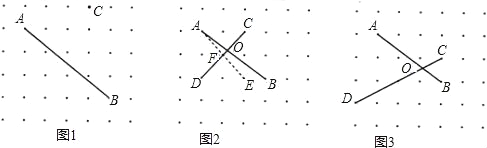
小明观察一个由1×1正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1,他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出它们相交所成锐角的正切值.
请回答:
(1)如图1,A,B,C是点阵中的三个点,请在点阵中找到点D,作出线段CD,使得CD⊥AB;
(2)如图2,线段AB与CD交于点O.为了求出∠AOD的正切值,小明在点阵中找到了点E,连接AE,恰好满足AE⊥CD于点F,再作出点阵中的其它线段,就可以构造相似三角形,经过推理和计算能够使问题得到解决.
请你帮小明计算:OC= ;tan∠AOD= ;
解决问题:
如图3,计算:tan∠AOD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
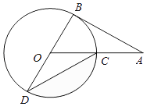
【题目】如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
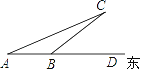
【题目】如图,一艘轮船以18海里/时的速度由西向东航行,在A处测得小岛C在北偏东75°方向上,两小时后,轮船在B处测得小岛C在北偏东60°方向上,在小岛周围15海里处有暗礁,若轮船仍然按18海里/时的速度向东航行,请问是否有触礁危险?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场设定了一个可以自由转动的转盘(转盘被等分成16个扇形),并规定:顾客在商场消费每满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄和蓝色区域,顾客就可以分别获得50元、30元和10元的购物券.如果顾客不愿意转转盘,则可以直接获得购物券15元.
(1)转动一次转盘,获得50元、30元、10元购物券的概率分别是多少?
(2)如果有一名顾客在商场消费了200元,通过计算说明转转盘和直接获得购物券,哪种方式对这位顾客更合算?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队合作完成一项工程,需要12天完成,工程费用共36000元,若甲、乙两工程队单独完成此项工程,乙工程队所用的时间是甲工程队的1.5倍,乙工程队每天的费用比甲工程队少800元.
(1)问甲、乙两工程队单独完成此项工程各需多少天?
(2)若让一个工程队单独完成这项工程,哪个工程队的费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
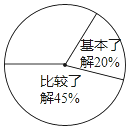
【题目】某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为多少人,表中m的值为多少;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,分别以AB、BC、DC为边向外作正方形,它们的面积分别为S1、S2、S3.若S2=48,S3=9,则S1的值为( )
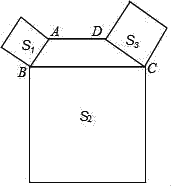
A. 18 B. 12 C. 9 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com