
【题目】阅读下面材料:
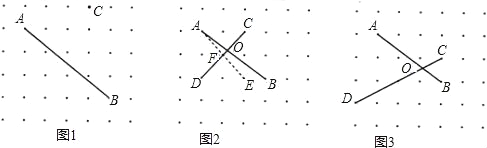
小明观察一个由1×1正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1,他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出它们相交所成锐角的正切值.
请回答:
(1)如图1,A,B,C是点阵中的三个点,请在点阵中找到点D,作出线段CD,使得CD⊥AB;
(2)如图2,线段AB与CD交于点O.为了求出∠AOD的正切值,小明在点阵中找到了点E,连接AE,恰好满足AE⊥CD于点F,再作出点阵中的其它线段,就可以构造相似三角形,经过推理和计算能够使问题得到解决.
请你帮小明计算:OC= ;tan∠AOD= ;
解决问题:
如图3,计算:tan∠AOD= .
【答案】(1)见解析;(2)![]() ;5;解决问题:
;5;解决问题:![]() .
.
【解析】
(1)用三角板过C作AB的垂线,从而找到D的位置;
(2)连接AC、DB、AD、DE.由△ACO∽△DBO求得CO的长,由等腰直角三角形的性质可以求出AF,DF的长,从而求出OF的长,在Rt△AFO中,根据锐角三角函数的定义即可求出tan∠AOD的值;
(3)如图,连接AE、BF,则AF=![]() ,AB=
,AB=![]() ,由△AOE∽△BOF,可以求出AO=
,由△AOE∽△BOF,可以求出AO=![]() ,在Rt△AOF中,可以求出OF=
,在Rt△AOF中,可以求出OF=![]() ,故可求得tan∠AOD.
,故可求得tan∠AOD.
解:(1)如图所示:
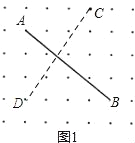
线段CD即为所求.
(2)如图2所示连接AC、DB、AD.
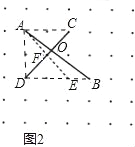
∵AD=DE=2,
∴AE=2![]() .
.
∵CD⊥AE,
∴DF=AF=![]() .
.
∵AC∥BD,
∴△ACO∽△DBO.
∴CO:DO=2:3.
∴CO=![]() .
.
∴DO=![]() .
.
∴OF=![]() .
.
tan∠AOD=![]() = 5.
= 5.
解决问题:如图3所示:
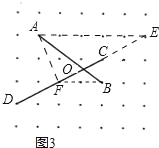
根据图形可知:BF=2,AE=5.
由勾股定理可知:AF=![]() =
=![]() ,AB=
,AB=![]() =
=![]() .
.
∵FB∥AE,
∴△AOE∽△BOF.
∴AO:OB=AE:FB=5:2.
∴AO=![]() .
.
在Rt△AOF中,OF=![]() =
=![]() .
.
∴tan∠AOD=![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
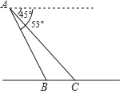
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为53°和45°,已知大桥BC与地面在同一水平面上,其长度为75m,请求出热气球离地面的高度.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
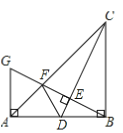
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:①![]() ②若点D是AB的中点,则AF=
②若点D是AB的中点,则AF=![]() AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若
AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若![]() ,则
,则![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
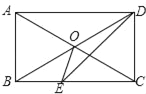
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
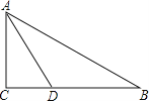
【题目】如图,在![]() 中,
中,![]() ,点D在边
,点D在边![]() 上,
上,![]() ,
,![]() ,点D到
,点D到![]() 的距离为3,下列说法中:①
的距离为3,下列说法中:①![]() 是
是![]() 的平分线;②
的平分线;②![]() 是等腰三角形;③点D在
是等腰三角形;③点D在![]() 的中垂线上;④
的中垂线上;④![]() :
:![]() :3,其中说法正确的是 ______
:3,其中说法正确的是 ______ ![]() 把所有正确结论的序号都写在横线上)
把所有正确结论的序号都写在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移10cm,如图2,OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是( )
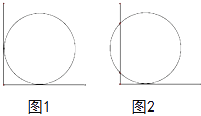
A. 25cm B. 30cm C. 50cm D. 60cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴相交于点A,与直线
与x轴相交于点A,与直线![]() 相交于点P.
相交于点P.
(1)求点P的坐标.
(2)请判断△OPA的形状并说明理由.
(3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.求S与t之间的函数关系式.
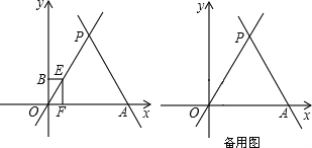
查看答案和解析>>
科目:初中数学 来源: 题型:
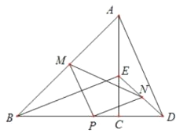
【题目】如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.
(1)试判断△PMN的形状,并证明你的结论;
(2)若CD=5,AC=12,求△PMN的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com