
【题目】凸四边形ABCD的两条对角线和两条边的长度都为1,则四边形ABCD中最大内角度数为( )
A.150°B.135°C.120°D.105°
【答案】A
【解析】
首先,这两条相等的边不可能是对边,如果两条对边相等,则对角线至少有一条大于这两条边.也就是说这两条相等的边是邻边(设为AB、AC),加上连接这两条边的那条对角线(BC),就是一个等边三角形(ABC);当另一条对角线(AD)垂直于对角线(BC)时,∠BDC是最大内角150°;当AD不垂直于BC时,∠BDC介于150°到90°之间,而∠ABD和∠ACD都介于75°到150°之间.所以最大的内角是150°.
解:如图:

∵AB=AC=BC,
∴△ABC是等边三角形,
当另一条对角线AD⊥BC时,∠BDC=150°;
当AD不垂直于BC时,∠BDC介于150°到90°之间,而∠ABD和∠ACD都介于75°到150°之间.
所以最大的内角是150°.
故选:A.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
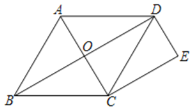
【题目】如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.
(1)求证:四边形DECO是矩形;
(2)连接AE交BD于点F,当∠ADB=30°,DE=3时,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上.已知α=36°,求长方形卡片的周长.
(精确到1mm,参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中:①当x>0时,y>0;②若a=﹣1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )
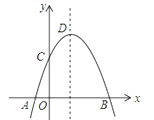
A. ① B. ② C. ③ D. ①②③都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
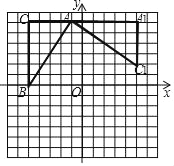
【题目】如图,△A1AC1是由△ABC绕某点P按顺时针方向旋转90°得到的,△ABC的顶点坐标分A(﹣1,6),B(﹣5,0),C(﹣5,6).
(1)求旋转中心P和点A1,C1的坐标;
(2)在所给网格中画出△A1AC1绕点P按顺时针方向旋转90°得到的图形;
(3)在所给网格中画出与△A1AC1关于点P成中心对称的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
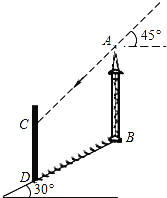
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com