
【题目】如图,![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 以
以![]() 的速度往返运动1次,
的速度往返运动1次,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,设点
,设点![]() 运动时间为
运动时间为![]() 秒
秒![]() .
.
![]()
(1)当![]() 时,求线段
时,求线段![]() 和
和![]() 的长度.
的长度.
(2)用含![]() 的代数式表示运动过程中
的代数式表示运动过程中![]() 的长.
的长.
(3)在运动过程中,若![]() 中点为
中点为![]() ,则
,则![]() 的长是否变化?若不变.求出
的长是否变化?若不变.求出![]() 的长;若发生变化,请说明理由.
的长;若发生变化,请说明理由.
【答案】(1)AB=6cm,CD=4.5cm;(2)①当0≤t≤5时, AB=3tcm, ②当5<t≤10时, AB=303tcm;(3)不变, 7.5cm.
【解析】
(1)根据速度×时间=路程,可得答案;根据线段的和差,可得BD的长,根据线段中点的性质,可得答案;
(2)此题分两情况:①A到D的过程中,根据速度×时间等路程,可得答案;②D返回A的过程中,根据线段的和差,可得AB的长;
(3)根据线段中点的性质,可得BE的长,BC的长,根据线段的和差,可得答案.
(1)当t=2时,AB=3×2=6(cm),
∵AB=6cm,AD=15cm,
∴BD=9cm,
∵C是线段BD的中点,
∴CD=4.5cm;
(2)∵![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 以
以![]() 的速度往返运动,
的速度往返运动,
①当0≤t≤5时,点B沿点A→D运动时,AB=3tcm,
②当5<t≤10时,点B沿点D→A运动时,AB=15-3(t-3)=303tcm;
(3)不变.
∵AB中点为E,C是线段BD的中点,
∴BE=![]() AB,BC=
AB,BC=![]() BD,
BD,
∴EC=![]() (AB+BD)
(AB+BD)
=![]() AD
AD
=![]() ×15
×15
=7.5(cm).


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现:如果每件童装降价1元,那么平均可多售出2件,设每件童装降价x元(x>0)时,平均每天可盈利y元.
(1)写出y与x的函数关系式;
(2)根(1)中你写出的函数关系式,解答下列问题:
①当该专卖店每件童装降价5元时,平均每天盈利多少元?
②当该专卖店每件童装降价多少元时,平均每天盈利400元?
③该专卖店要想平均每天盈利600元,可能吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为37°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB和楼房MN的高度.
(![]() ,
,![]() ,
,![]() ,
,![]() ,结果精确到0.1m)
,结果精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要设计一本书的封面,封面长为27cm,宽为21cm,正中央是一个与整个封面长宽比例相同的矩形.如果要使四周的彩色边衬等宽,且四周的彩色边衬所占面积是封面面积的四分之一,应如何设计四周边衬的宽度?(结果保留根号)

封面的长宽之比为27:21=9:7,中央矩形的长宽之比也应是9:7,若设上下边衬的宽均为9xcm,则左右边衬均为7xcm.
(1)用含x的代数式表示:中央矩形的长为______cm,宽为______cm,中央矩形的面积为______cm2.
(2)列出方程并完成本题解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B. 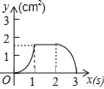 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,分别以BC,AB,AC为边作等边三角形BCE,ACF,ABD
(1)若存在四边形ADEF,判断它的形状,并说明理由.
(2)存在四边形ADEF的条件下,请你给△ABC添个条件,使得四边形ADEF成为矩形,并说明理由.
(3)当△ABC满足什么条件时四边形ADEF不存在.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com