
【题目】如图,要设计一本书的封面,封面长为27cm,宽为21cm,正中央是一个与整个封面长宽比例相同的矩形.如果要使四周的彩色边衬等宽,且四周的彩色边衬所占面积是封面面积的四分之一,应如何设计四周边衬的宽度?(结果保留根号)

封面的长宽之比为27:21=9:7,中央矩形的长宽之比也应是9:7,若设上下边衬的宽均为9xcm,则左右边衬均为7xcm.
(1)用含x的代数式表示:中央矩形的长为______cm,宽为______cm,中央矩形的面积为______cm2.
(2)列出方程并完成本题解答.
【答案】(1)(27-18x);(21-14x);(27-18x)(21-14x);(2)上下边衬的宽为:![]() cm,左右边衬的宽为:
cm,左右边衬的宽为:![]() cm.
cm.
【解析】
(1)设上下边衬的宽均为9xcm,则左右边衬均为7xcm.根据中央矩形的长=封面的长-2×上下边衬的宽,中央矩形的宽=封面的宽-2×左右边衬的宽,再根据矩形的面积=长×宽列式即可;
(2)由于四周的彩色边衬所占面积是封面面积的四分之一,所以中央矩形的面积是封面面积的四分之三,据此列出方程,求解即可.
解:(1)设上下边衬的宽均为9xcm,则左右边衬均为7xcm.
∵一本书的封面长为27cm,宽为21cm,
∴中央矩形的长为(27-18x)cm,宽为(21-14x)cm,中央矩形的面积为(27-18x)(21-14x)cm2.
故答案为(27-18x),(21-14x)cm,(27-18x)(21-14x);
(2)由题意,得(27-18x)(21-14x)=![]() ×27×21,
×27×21,
解得x1=![]() ,x2=
,x2=![]() (不合题意舍去).
(不合题意舍去).
∴上下边衬的宽为:![]() cm,
cm,
左右边衬的宽为:![]() cm.
cm.


 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与反比例函数
与反比例函数![]() (
(![]() )图像交于点A,将直线向右平移4个单位,交反比例函数
)图像交于点A,将直线向右平移4个单位,交反比例函数![]() (
(![]() )图像于点B,交y轴于点C,连结AB、AC,则△ABC的面积为_______.
)图像于点B,交y轴于点C,连结AB、AC,则△ABC的面积为_______.
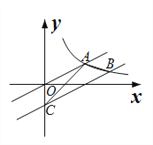
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
幻方的历史很悠久,传说中最早出现在夏禹时代的“洛书”,用今天的数学符号翻译出来,就是一个三阶幻方,即将若干个数组成一个正方形数阵,任意一行、一列及对角线上的数字之和都相等.如图1,就是一个三阶幻方,由1,2,3,4,5,6,7,8,9九个数字组成的一个三行三列的矩阵(如图),其对角线、横行、纵向的和都为15.
(1)探究:研究发现三阶幻方中间的数字与9个数的和有确定的数量关系.如果设数字连续性三阶幻方中间的数字是a,则幻方中9个数字之和是 (用含a的字母代数式表示)
(2)应用:请你选取一组数据构造一个三阶幻方,填入到如图2的3×3方格中,使得每行、每列、每条对角线上的三个数之和都等于21;


(3)拓展:
数阵是由幻方演化出来的另一种数字图.将连续的奇数1,3,5,7,9…排列成数阵(如图3),用十字框随机框出5个数,十字框中的五数之和能等于2020吗?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“不忘初心,牢记使命.”全面建设小康社会到了攻坚克难阶段. 为了解2017年全国居民收支数据国家统计局组织实施了住户收支与生活状况调查,按季度发布.调查采用分层、多阶段、与人口规模大小成比例的概率抽样方法,在全国31个省(区、市)的1650个县(市、区)随机抽选16万个居民家庭作为调查户.已知2017年前三季度居民人均消费可支配收入平均数是2016年前三季度居民人均消费可支配收入平均数的115%,人均消费支出为11423元,根据下列两个统计图回答问题:(以下计算最终结果均保留整数)

(1)求年度调查的样本容量及2017年前三季度居民人均消费可支配收入平均数(元);
(2)求在2017年前三季度居民人均消费支出中用于医疗保健所占圆心角度数;
(3)求在2017年前三季度居民人均消费支出中用于居住的金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 以
以![]() 的速度往返运动1次,
的速度往返运动1次,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,设点
,设点![]() 运动时间为
运动时间为![]() 秒
秒![]() .
.
![]()
(1)当![]() 时,求线段
时,求线段![]() 和
和![]() 的长度.
的长度.
(2)用含![]() 的代数式表示运动过程中
的代数式表示运动过程中![]() 的长.
的长.
(3)在运动过程中,若![]() 中点为
中点为![]() ,则
,则![]() 的长是否变化?若不变.求出
的长是否变化?若不变.求出![]() 的长;若发生变化,请说明理由.
的长;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的括号里-2,100π,-5![]() ,0.8,-|+5.2|,0,0.1010010001…,-(-4
,0.8,-|+5.2|,0,0.1010010001…,-(-4![]() )
)
正有理数集合:{ }
整数集合:{ }
负分数集合:{ }
无理数集合:{ }
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
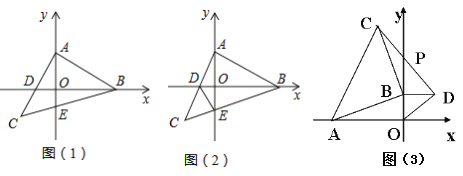
(1)如图(1),已知C点的横坐标为-1,直接写出点A的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图(3), 若点A在x轴上,且A(-4,0),点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连结CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,抛物线对称轴为x=﹣![]() ,下列结论中,错误的结论是( )
,下列结论中,错误的结论是( )
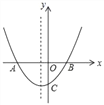
A. abc>0
B. 方程ax2+bx+c=0的解是x1=﹣2,x2=1
C. b2﹣4ac>0
D. a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下:
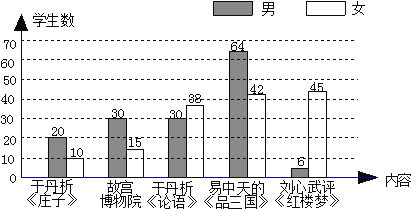
请根据统计图提供的信息回答以下问题:
(1)这一调查属于_______(选填“抽样调查”或“普查”),抽取的学生数为_____名;
(2)估计喜欢收听易中天《品三国》的学生约占全校学生的____%(精确到小数点后一位);
(3)已知该校女学生共有1800名,则该校喜欢收听刘心武评《红楼梦》的女学生大约有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com