
分析 (1)利用单项式的除法法则即可直接求解;
(2)首先计算乘方,然后进行除法运算即可;
(3)首先计算乘方,然后进行除法运算,最后进行乘法计算即可.
解答 解:(1)原式=-$\frac{27}{8}$×$\frac{16}{9}$y2z4=-6y2z4;
(2)原式=81x12y12z4÷9x6y4z2÷$\frac{1}{2}$x2y6z=18x4y2z;
(3)原式=$\frac{9}{5}$a8x6y4÷$\frac{1}{2}$a4xy2•4a2x2=$\frac{18}{5}$a4x5y2•4a2x2=$\frac{72}{5}$a6x7y2.
点评 本题考查单项式的混合运算,正确分清运算顺序,理解字母指数的变化是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
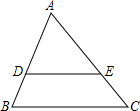 如图,△ABC中,DE∥BC,且DE:BC=2:3,则下列结论一定正确的是( )
如图,△ABC中,DE∥BC,且DE:BC=2:3,则下列结论一定正确的是( )| A. | AD:DE=2:3 | B. | AD:BD=2:3 | C. | AD:AE=2:3 | D. | AD:AB=2:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有理数x、y在数轴上对应点如图所示:
有理数x、y在数轴上对应点如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
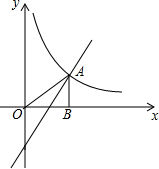 一次函数y=kx-1与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点A,过点A作AB⊥x轴于点B,已知S△AOB=1,求反比例函数及一次函数的表达式.
一次函数y=kx-1与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点A,过点A作AB⊥x轴于点B,已知S△AOB=1,求反比例函数及一次函数的表达式.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
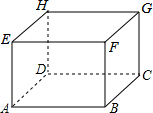 如图,一个上方无盖的长方体盒子紧贴地面,一只蚂蚁由盒外A处出发,沿着盒子面爬行到盒内的点B处,已知,AB=9,BC=9,BF=6,这只蚂蚁爬行的最短距离是15.
如图,一个上方无盖的长方体盒子紧贴地面,一只蚂蚁由盒外A处出发,沿着盒子面爬行到盒内的点B处,已知,AB=9,BC=9,BF=6,这只蚂蚁爬行的最短距离是15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
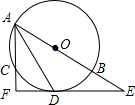 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB、AC的延长线于点E、F.求证:AF+CF=AB.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB、AC的延长线于点E、F.求证:AF+CF=AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com