
【题目】如图,AB是⊙O直径,直径AB⊥弦CD于点E,四边形ADCF是平行四边形,CD=4![]() ,BE=2.
,BE=2.

(1)求⊙O直径和弦AD的长;
(2)求证:FC是⊙O切线.
【答案】(1)⊙O直径为8,弦AD长为4![]() .(2)见解析
.(2)见解析
【解析】
试题分析:(1)设⊙O的半径为r,连接OC,则OC=r,OE=r﹣2,根据垂径定理得到CE=![]() CD=2
CD=2![]() ,然后根据勾股定理得到r2=(r﹣2)2+(2
,然后根据勾股定理得到r2=(r﹣2)2+(2![]() )2,求得r=4,从而求得AE=6,在Rt△AED中,根据勾股定理即可求得AD;
)2,求得r=4,从而求得AE=6,在Rt△AED中,根据勾股定理即可求得AD;
(2)连结OF,由四边形ABCD是平行四边形得到AF∥DC,则AB⊥AF,即:∠FAO=90°,然后证得平行四边形ADCF是菱形,得出FC=AF,证得△FCO≌△FAO,得出根据切线的判定得到∠FCO=∠FAO=90°,即可证得FC为⊙O的切线.
解:(1)设⊙O的半径为r,连接OC,则OC=r,OE=r﹣2
∵直径AB⊥弦CD
∴CE=![]() CD=
CD=![]() ×4
×4![]() =2
=2![]() ,
,
在Rt△OCE中:OC2=CE2+OE2 即:r2=(r﹣2)2+(2![]() )2,
)2,
解得:r=4,
∴AE=2×4﹣2=6,
在Rt△AED中:AD=![]() =
=![]() =4
=4![]() ,
,
∴⊙O直径为8,弦AD长为4![]() .
.
(2)连结OF,
∵平行四边形ADCF中AF∥CD
又∵AB⊥CD,
∴AB⊥AF,即:∠FAO=90°,
由(1)可知AD=CD=4![]() ,
,
∴平行四边形ADCF是菱形,
∴FC=AF,
在△FCO和△FAO中,
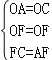
∴△FCO≌△FAO(SSS),
∴∠FCO=∠FAO=90°即:OC⊥FC
∴FC是⊙O切线.



科目:初中数学 来源: 题型:
【题目】到一个三角形三个顶点的距离都相等的点是这个三角形的( )
A. 三条中线的交点 B. 三条角平分线的交点
C. 三条高的交点 D. 三条边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.

(1)求证:BE=BF;
(2)若△ABC的面积为70,AB=16,DE=5,则BC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】所谓配方,就是把一个多项式经过适当变形配成完全平方式.配方法除一元二次方程求根公式推导这一典型应用外,在因式分解、化简二次根式、证明恒等式、解方程、求代数式最值等问题中都有广泛应用.是一种很重要、很基本的数学方法.如以下例1,例2:
例1:分解因式 x2﹣120x+3456
解:原式=x2﹣120x+3600+3456﹣3600
=(x﹣60)2﹣144
=(x﹣60+12)(x﹣60﹣12)
=(x﹣48)(x﹣72)
例2:化简:![]()
解:原式=![]()
=![]()
=![]() ﹣
﹣![]()
阅读以上材料,请问答以下问题:
(1)分解因式:x2﹣40x+319= ;
(2)化简:![]() ;
;
(3)利用配方法求4x2+y2﹣2y﹣4x+15的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房200间供游客居住,当每间客房的定价为每天180元时,客房恰好全部住满;如果每间客房每天的定价每增加10元,就会减少4间客房出租.设每间客房每天的定价增加![]() 元,宾馆出租的客房为
元,宾馆出租的客房为![]() 间.求:
间.求:
(1)![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果某天宾馆客房收入38400元,那么这天每间客房的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形两边长分别是2 cm和5 cm,则这个三角形周长是( )
A. 9 cm B. 12 cm C. 9 cm或12 cm D. 14 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
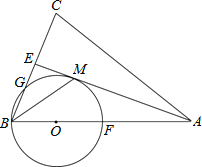
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com