
 ��ͼ����ƽ��ֱ������ϵxOy�У���֪�ı���DOBC�Ǿ��Σ���D��O��4����B��6��0����������������y=$\frac{{k}_{1}}{x}$��x��0����ͼ���߶�OC���е�A���ֱ�DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b
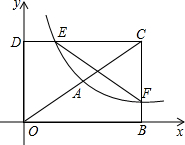
��ͼ����ƽ��ֱ������ϵxOy�У���֪�ı���DOBC�Ǿ��Σ���D��O��4����B��6��0����������������y=$\frac{{k}_{1}}{x}$��x��0����ͼ���߶�OC���е�A���ֱ�DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b���� ��1�������þ��ε��������C�����꣬�������߶��е����깫ʽ���ɵ�A��3��2�����ٰ�A���������y=$\frac{{k}_{1}}{x}$��x��0�������k1=6���Ӷ��õ���������������ʽΪy=$\frac{6}{x}$��Ȼ�����÷���������ͼ���ϵ�������������E���F�����꣬�����ô���ϵ������ֱ��EF�Ľ���ʽ��
��2���۲캯��ͼ��д��һ�κ���ͼ���ڷ���������ͼ���Ϸ�����Ӧ���Ա�����ȡֵ��Χ���ɣ�
��3�������÷���������k�ļ�������õ�S��OED=S��OBF=3���ټ����CE=$\frac{9}{2}$��FC=3�����Ÿ��������������ʽ�����S��CEF=$\frac{27}{4}$������������ĺͲ�õ�S��OEF=$\frac{45}{4}$����P������Ϊ��0��m�������������������ʽ�õ�$\frac{1}{2}$•|m|•$\frac{3}{2}$=$\frac{45}{4}$�����m=��15���Ӷ��ɵ�P�����꣮
��� 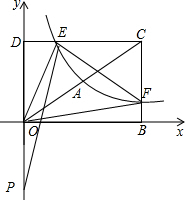 �⣺��1����D��0��4����B��6��0����
�⣺��1����D��0��4����B��6��0����
��C��6��4����
���߶�OC���е�A������Ϊ��3��2����
��A��3��2������y=$\frac{{k}_{1}}{x}$��x��0����k1=3��2=6��
�෴������������ʽΪy=$\frac{6}{x}$��
��y=4ʱ��$\frac{6}{x}$=4�����x=$\frac{3}{2}$����E��$\frac{3}{2}$��4����
��x=6ʱ��y=$\frac{6}{x}$=1����F��6��1����
��E��$\frac{3}{2}$��4����F��6��1���ֱ����y=k2x+b��$\left\{\begin{array}{l}{\frac{3}{2}{k}_{2}+b=4}\\{6{k}_{2}+b=1}\end{array}\right.$�����$\left\{\begin{array}{l}{{k}_{2}=-\frac{2}{3}}\\{b=5}\end{array}\right.$��
��ֱ��EF�Ľ���ʽΪy=-$\frac{2}{3}$x+5��
��2��$\frac{3}{2}$��x��6��
��3�����ڣ�
�ߵ�E��F���ڷ���������ͼ���ϣ�
��S��OED=S��OBF=$\frac{1}{2}$��6=3��
��E��$\frac{3}{2}$��4����F��6��1����
��CE=6-$\frac{3}{2}$=$\frac{9}{2}$��FC=3��
��S��CEF=$\frac{1}{2}$��3��$\frac{9}{2}$=$\frac{27}{4}$��
��S��OEF=4��6-3-3-$\frac{27}{4}$=$\frac{45}{4}$��
��P��������0��m����
��$\frac{1}{2}$•|m|•$\frac{3}{2}$=$\frac{45}{4}$�����m=��15��
������������P��������0��15����0��-15����
���� ���⿼���˷�����������һ�κ����Ľ������⣺����������һ�κ����Ľ������꣬������������ϵʽ�����ɷ�������⣬���������н��������н��㣬�������⣬���������㣮Ҳ�����˷���������ͼ���ϵ�����������������������ʽ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16 | B�� | 8 | C�� | 8��$\sqrt{22}$ | D�� | 16��$\sqrt{22}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 5 | C�� | 8 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
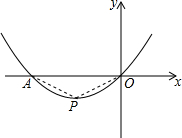 ��֪������y=ax2+bx+c��a��0����ͼ��ԭ��O����x���ڵ�A���䶥��P������Ϊ��-$\sqrt{3}$��-1��
��֪������y=ax2+bx+c��a��0����ͼ��ԭ��O����x���ڵ�A���䶥��P������Ϊ��-$\sqrt{3}$��-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
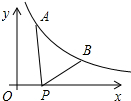 ��ͼ��ʾ����֪A��0.2��y1����B��2��y2��Ϊ����������y=$\frac{1}{x}$ ͼ���ϵ����㣬����P��x��0����x�����������˶������߶�AP���߶�BP֮��ﵽ���ʱ����P�������ǣ�������
��ͼ��ʾ����֪A��0.2��y1����B��2��y2��Ϊ����������y=$\frac{1}{x}$ ͼ���ϵ����㣬����P��x��0����x�����������˶������߶�AP���߶�BP֮��ﵽ���ʱ����P�������ǣ�������| A�� | ��0.5��0�� | B�� | ��1��0�� | C�� | ��1.5��0�� | D�� | ��2.5��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����������ABCDEF��ֱ������ϵ�ڵ�λ����ͼ��ʾ��A��-2��0������B��ԭ�㣬����������ABCDEF��x����������������������ת��ÿ�η�ת60�㣬����2015�η�ת֮��B�������ǣ�4031��$\sqrt{3}$����
��֪����������ABCDEF��ֱ������ϵ�ڵ�λ����ͼ��ʾ��A��-2��0������B��ԭ�㣬����������ABCDEF��x����������������������ת��ÿ�η�ת60�㣬����2015�η�ת֮��B�������ǣ�4031��$\sqrt{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com