
分析 (1)应用树状图法,判断出甲胜出的概率是多少即可.
(2)首先对甲、乙、丙三名同学规定一个摸球顺序:丙→甲→乙,然后应用树状图法,判断出第一个摸球的丙同学和最后一个摸球的乙同学胜出的概率各等于多少即可.
(3)首先根据(1)(2),猜想这三名同学每人胜出的概率之间的大小关系为:P(甲胜出)=P(乙胜出)=P(丙胜出);然后总结出得到的活动经验为:抽签是公平的,与顺序无关.
解答 解:(1)如图1,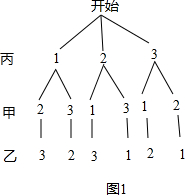 ,
,
甲胜出的概率为:
P(甲胜出)=$\frac{1}{3}$.
(2)如图2, ,
,
对甲、乙、丙三名同学规定一个摸球顺序:丙→甲→乙,
则第一个摸球的丙同学胜出的概率为:
P(丙胜出)=$\frac{6}{24}$=$\frac{1}{4}$,
则最后一个摸球的乙同学胜出的概率为:
P(乙胜出)=$\frac{6}{24}=\frac{1}{4}$.
(3)这三名同学每人胜出的概率之间的大小关系为:
P(甲胜出)=P(乙胜出)=P(丙胜出).
得到的活动经验为:抽签是公平的,与顺序无关.(答案不唯一)
故答案为:丙、甲、乙、$\frac{1}{4}、\frac{1}{4}$.
点评 此题主要考查了列表法与树状图法,要熟练掌握,解答此题的关键是要明确:(1)列举法(树形图法)求概率的关键在于列举出所有可能的结果,列表法是一种,但当一个事件涉及三个或更多元素时,为不重不漏地列出所有可能的结果,通常采用树形图.(2)树形图列举法一般是选择一个元素再和其他元素分别组合,依次列出,象树的枝丫形式,最末端的枝丫个数就是总的可能的结果n.(3)当有两个元素时,可用树形图列举,也可以列表列举.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
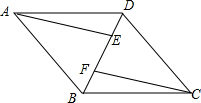 已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| 价格(万元/台) | a | b |
| 处理污水量(吨/月) | 250 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com