
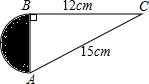
 求阴影部分的面积.
求阴影部分的面积. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
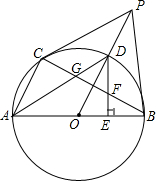 如图,AB为⊙O的直径,PB为⊙O的切线,AC∥OP,点C在⊙O上,OP交⊙O于D,DA交BC于G.
如图,AB为⊙O的直径,PB为⊙O的切线,AC∥OP,点C在⊙O上,OP交⊙O于D,DA交BC于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
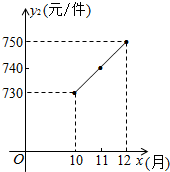 某企业为重庆计算机产业基地提供电脑配件,受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
某企业为重庆计算机产业基地提供电脑配件,受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
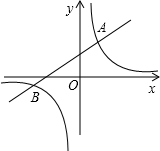 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
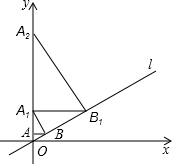 如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂 线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为(0,42015)或(0,24030).
如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂 线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为(0,42015)或(0,24030).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com