
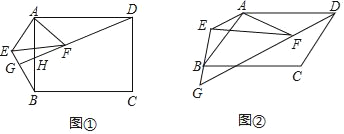
【题目】探究:如图①,在矩形ABCD中,以点A为直角顶点作Rt△AEF,连结BE、DF,直线DF交直线BE于点G,DG与AB交于点H,且![]() .
.
(1)求证:△ABE∽△ADF.
(2)求证:DG⊥BE;
拓展:如图②,在ABCD中,以点A为顶点作∠EAF=∠BAD,连结BE、DF,直线DF交直线BE于点G,且![]() ,若∠BCD=130°,则∠EGD的大小为 度.
,若∠BCD=130°,则∠EGD的大小为 度.
【答案】(1)△ABE∽△ADF;(2)50.
【解析】
探究:(1)根据矩形的性质得到∠BAD=90°,根据余角的性质得到∠EAB=∠DAF,根据相似三角形的判定定理即可得到结论;
(2)根据相似三角形的性质得到∠ADF=∠ABE,根据对顶角相等得到∠AHD=∠BHG,根据三角形的内角和即可得到结论;拓展:根据平行四边形的性质得到AB∥CD,AD∥BC,求得∠ABC=180°-∠C=50°,∠ADF=∠2,根据相似三角形的性质得到∠ADF=∠3,根据三角形的内角和和平角的定义即可得到结论.
探究:(1)在矩形ABCD中,
∵∠BAD=90°,
∵∠AEF=90°,
∴∠EAB+∠BAF=∠DAF+∠BAF=90°,
∴∠EAB=∠DAF,
∵![]() ,
,
∴△ABE∽△ADF;
(2)∵△ABE∽△ADF,
∴∠ADF=∠ABE,
设AB与DG的交点为H,
∵∠AHD=∠BHG,
∴∠BGH=180°﹣∠ABG﹣∠BHG=180°﹣∠AHF﹣∠ADF=∠BAD=90°,
∴DG⊥BE;
拓展:在ABCD中,
∵AB∥CD,AD∥BC,
∴∠ABC=180°﹣∠C=50°,∠ADF=∠2,
∵∠EAF=∠BAD,
∴∠EAF﹣∠BAF=∠BAD﹣∠BAF,
即∠EAB=∠DAF,
∵![]() ,
,
∴△ABE∽△ADF,
∴∠ADF=∠3,
∴∠2=∠3,
∵∠ABC=180°﹣∠GBC﹣∠3,∠EGD=180°﹣∠GBD﹣∠2,
∴∠EGD=∠ABC=50°,
故答案为:50.


科目:初中数学 来源: 题型:
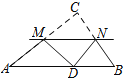
【题目】如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在边AB上的点D处,已知MN∥AB,MC=6,NC=2![]() ,则四边形MABN的面积是___________.
,则四边形MABN的面积是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列格式, ![]() -
- ![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
(1)化简以上各式,并计算出结果;
(2)以上格式的结果存在一定的规律,请按规律写出第5个式子及结果.
(3)用含n(n≥1的整数)的式子写出第n个式子及结果,并给出证明的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
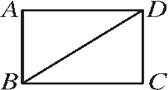
【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形(长方形)ABCD沿EF折叠,使点B与点D重合,点A落在G处,连接BE,DF,则下列结论:①DE=DF,②FB=FE,③BE=DF,④B、E、G三点在同一直线上,其中正确的是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若等腰三角形的一个内角是![]() 则它的另外两个内角的度数是__________,若等腰三角形的一个内角是
则它的另外两个内角的度数是__________,若等腰三角形的一个内角是![]() ,则它的另外两个内角的度数__________.
,则它的另外两个内角的度数__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com