
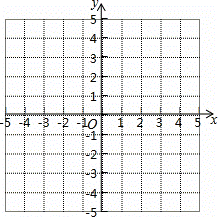
如图,已知在平面直角坐标系xOy中,抛物线y=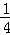 x2+bx+c与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,﹣3),且OA=2OC.
x2+bx+c与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,﹣3),且OA=2OC.
(1)求这条抛物线的表达式及顶点M的坐标;
(2)求tan∠MAC的值;
(3)如果点D在这条抛物线的对称轴上,且∠CAD=45°,求点D的坐标.
解:(1)∵C(0,﹣3),
∴OC=3.y=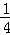 x2+bx﹣3.
x2+bx﹣3.
∵OA=2OC,
∴OA=6.
∵a=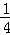 >0,点A在点B右侧,抛物线与y轴交点C(0,﹣3).
>0,点A在点B右侧,抛物线与y轴交点C(0,﹣3).
∴A(6,0).
∴0=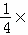 36+6b﹣3,
36+6b﹣3,
∴b=﹣1.
∴y=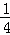 x2﹣x﹣3,
x2﹣x﹣3,
∴y=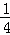 (x﹣2)2﹣4,
(x﹣2)2﹣4,
∴M(2,﹣4).
答:抛物线的解析式为y=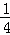 x2﹣x﹣3,M的坐标为(2,﹣4);
x2﹣x﹣3,M的坐标为(2,﹣4);
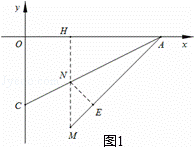
(2)如图1,过点M作MH⊥x轴,垂足为点H,交AC于点N,过点N作NE⊥AM于点E,垂足为点E.
∴∠AHM=∠NEM=90°.
在Rt△AHM中,HM=AH=4,由勾股定理,得
AM=4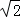 ,
,
∴∠AMH=∠HAM=45°.
设直线AC的解析式为y=kx+b,由题意,得
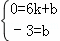 ,
,
解得: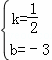 ,
,
∴直线AC的表达式为y=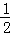 x﹣3.
x﹣3.
当x=2时,y=﹣2,
∴N(2,﹣2).
∴MN=2.
∵∠NEM=90°,∠NME=45°,
∴∠MNE=∠NME=45°,
∴NE=ME.
在Rt△MNE中,
∴NE2+ME2=NM2,
∴ME=NE=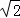 .
.
∴AE=AM﹣ME=3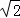
在Rt△AEN中,tan∠MAC=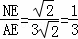 .
.
答:tan∠MAC= ;
;
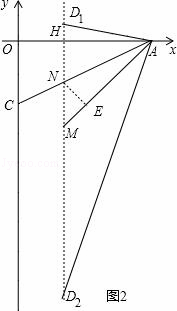
(3)如图2,①当D点在AC上方时,
∵∠CAD1=∠D1AH+∠HAC=45°,且∠HAM=∠HAC+∠CAM=45°,
∴∠D1AH=∠CAM,
∴tan∠D1AH=tan∠MAC= .
.
∵点D1在抛物线的对称轴直线x=2上,
∴D1H⊥AH,
∴AH=4.
在Rt△AHD1中,
D1H=AH•tan∠D1AH=4×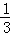 =
=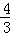 .
.
∴D1(2,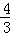 );
);
②当D点在AC下方时,
∵∠D2AC=∠D2AM+∠MAC=45°,且∠AMH=∠D2AM+∠AD2M=45°,
∴∠MAC=∠AD2M.
∴tan∠AD2H=tan∠MAC=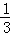 .
.
在Rt△D2AH中,D2H=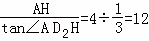 .
.
∴D2(2,﹣12).
综上所述:D1(2,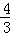 );D2(2,﹣12).
);D2(2,﹣12).


科目:初中数学 来源: 题型:
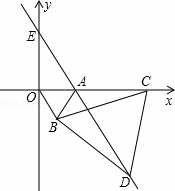
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
①△OBC与△ABD全等吗?判断并证明你的结论;
②随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:
①当x>3时,y<0;
②3a+b>0;
③﹣1≤a≤﹣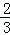 ;
;
④3≤n≤4中,
正确的是( )
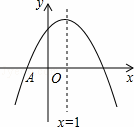
A. ①② B. ③④ C. ①④ D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com