

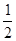 ∠CO2D=30°,在Rt△O1AO2中,根据∠AO2O1的正弦函数可表示出O1O2的长,从而得到结果;
∠CO2D=30°,在Rt△O1AO2中,根据∠AO2O1的正弦函数可表示出O1O2的长,从而得到结果;
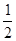 ∠CO2D=30°.
∠CO2D=30°. ,
,


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
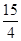 ,以O为圆心,OA为半径作圆.
,以O为圆心,OA为半径作圆.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A. | B. | C.2 | D.3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
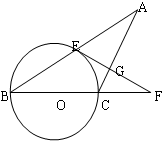
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 cm的⊙O从斜坡上的A点处沿斜坡滚动到平地上的C点处,已知∠ABC=120°,AB="10" cm,BC=20cm,那么圆心O运动所经过的路径长度为
cm的⊙O从斜坡上的A点处沿斜坡滚动到平地上的C点处,已知∠ABC=120°,AB="10" cm,BC=20cm,那么圆心O运动所经过的路径长度为
| A.30 cm | B.29 cm | C.28 cm | D.27 cm cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com