
【题目】在平面直角坐标系xOy中,一次函数![]() 的图象与直线
的图象与直线![]() 平行,且经过点A(1,6).
平行,且经过点A(1,6).
(1)求一次函数![]() 的解析式;
的解析式;
(2)求一次函数![]() 的图象与坐标轴围成的三角形的面积.
的图象与坐标轴围成的三角形的面积.
【答案】(1) y=2x+4 ;(2)直线y=2x+4与坐标轴围成的三角形的面积为![]()
【解析】
(1)根据函数y=kx+b的图象与直线y=2x平行,且经过点A(1,6),即可得出k和b的值,即得出了函数解析式.
(2)先求出与x轴及y轴的交点坐标,然后根据三角形面积公式求解即可.
(1)∵一次函数y=kx+b的图象为直线,且与直线y=2x平行,
∴k=2
又知其过点A(1,6),
∴2+b=6
∴b=4.
∴一次函数的解析式为y=2x+4
(2)当x=0时,y=4,
可知直线y=2x+4与y轴的交点为(0,4)
当y=0时,x=-2,
可知直线y=2x+4与x轴交点为(-2,0)
可得该直角三角形的两条直角边长度分别为4和2.
所以直线y=2x+4与坐标轴围成的三角形的面积为![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
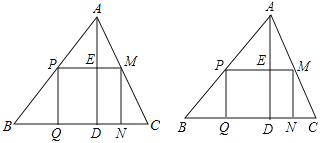
【题目】如图:有一块余料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm.
(1)如果把它加工成长方形零件,使长方形的一边在BC上,其余两个顶点分别在AB、AC上,设长方形宽xmm,面积为ymm2,那么宽为多少时,其面积最大.最大面积是多少?
(2)若以BC的中点O为原点建立平面直角坐标系,B(-60,0),AD=BD.
求过A、B、C三点的抛物线解析式;
在此抛物线对称轴上是否存在一点R,使以A、B、R为顶点的三角形是直角三角形.若存在,请直接写出R点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
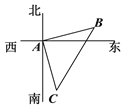
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水稻种植是嘉兴的传统农业.为了比较甲、乙两种水稻秧苗的长势,农技人员从两块试验田中分别随机抽取5株水稻秧苗,将测得的苗高数据绘制成如图所示的统计图.
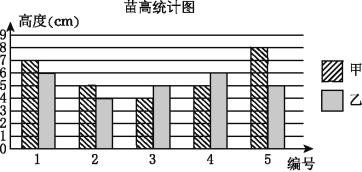
请你根据统计图所提供的数据,计算甲、乙两种水稻苗高的平均数和方差,并比较两种水稻的长势.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学中,运用整体思想方法在求代数式的值中非常重要.
例如:已知:a2+2a=1,则代数式2a2+4a+4=2( a2+2a) +4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)若![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,代数式
时,代数式![]() 的值是5,求当
的值是5,求当![]() 时,代数式px3+qx+1的值;
时,代数式px3+qx+1的值;
(3)当![]() 时,代数式
时,代数式![]() 的值为m,求当
的值为m,求当![]() 时,求代数式
时,求代数式![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“摩拜单车”公司调查无锡市民对其产品的了解情况,随机抽取部分市民进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制了如下尚不完整的统计图.
.根据调查结果绘制了如下尚不完整的统计图.
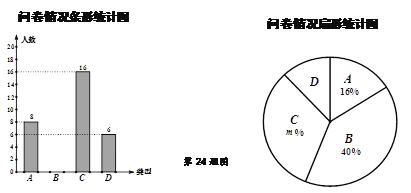
(1)本次问卷共随机调查了 名市民,扇形统计图中![]() .
.
(2)请根据数据信息补全条形统计图.
(3)扇形统计图中“D类型”所对应的圆心角的度数是 .
(4)从这次接受调查的市民中随机抽查一个,恰好是“不了解”的概率是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com