
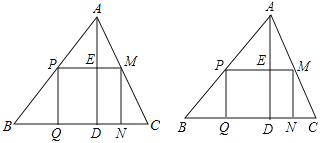
ЎҫМвДҝЎҝИзНјЈәУРТ»ҝйУаБПөДРОЧҙКЗИсҪЗИэҪЗРОABCЈ¬ұЯBC=120mmЈ¬ёЯAD=80mmЈ®
ЈЁ1Ј©Из№ы°СЛьјУ№ӨіЙіӨ·ҪРОБгјюЈ¬К№іӨ·ҪРОөДТ»ұЯФЪBCЙПЈ¬ЖдУаБҪёц¶Ҙөг·ЦұрФЪABЎўACЙПЈ¬ЙиіӨ·ҪРОҝнxmmЈ¬Гж»эОӘymm2Ј¬ДЗГҙҝнОӘ¶аЙЩКұЈ¬ЖдГж»эЧоҙуЈ®ЧоҙуГж»эКЗ¶аЙЩЈҝ
(2Ј©ИфТФBCөДЦРөгOОӘФӯөгҪЁБўЖҪГжЦұҪЗЧшұкПөЈ¬BЈЁ-60Ј¬0Ј©Ј¬AD=BDЈ®
Зу№эAЎўBЎўCИэөгөДЕЧОпПЯҪвОцКҪЈ»
ФЪҙЛЕЧОпПЯ¶ФіЖЦбЙПКЗ·сҙжФЪТ»өгRЈ¬К№ТФAЎўBЎўRОӘ¶ҘөгөДИэҪЗРОКЗЦұҪЗИэҪЗРОЈ®ИфҙжФЪЈ¬ЗлЦұҪУРҙіцRөгөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј© өұxЈҪ40КұЈ¬yЧоҙуЦөЈҪ2400 Ј»ЈЁ2Ј©![]() Ј»ЈЁ3Ј©јыҪвОцЈ®
Ј»ЈЁ3Ј©јыҪвОцЈ®
ЎҫҪвОцЎҝ·ЦОцЈәЈЁ1Ј©ЙиPQ=xЈ¬АыУГПаЛЖИэҪЗРОөДРФЦКҝЙөГіцQN=©Ғ![]() x+120Ј¬ёщҫЭҫШРОөДГж»э№«КҪјҙҝЙөГіцy=©Ғ
x+120Ј¬ёщҫЭҫШРОөДГж»э№«КҪјҙҝЙөГіцy=©Ғ![]() x2+120xЈ¬Ед·ҪәујҙҝЙХТіцГж»эөДЧоҙуЦөЈ»
x2+120xЈ¬Ед·ҪәујҙҝЙХТіцГж»эөДЧоҙуЦөЈ»
ЈЁ2Ј©ўЩТАХХМвТв»ӯіцНјРОЈ¬УЙADөДіӨ¶ИҝЙөГіцөгAөДЧшұкЈ¬ёщҫЭөгAЎўBөДЧшұкЈ¬АыУГҙэ¶ЁПөКэ·ЁјҙҝЙЗуіцЕЧОпПЯөДҪвОцКҪЈ»
ўЪЙиөгRөДЧшұкОӘЈЁ0Ј¬nЈ©Ј¬ФтAB=80![]() Ј¬AR=
Ј¬AR=![]() Ј¬BR=
Ј¬BR=![]() Ј¬·ЦЎПABR=90ЎгЎўЎПARB=90ЎгәНЎПBAR=90ЎгИэЦЦЗйҝцҝјВЗЈ¬АыУГ№ҙ№Й¶ЁАнјҙҝЙөГіц№ШУЪnөДТ»ФӘТ»ҙОЈЁ»тТ»ФӘ¶юҙОЈ©·ҪіМЈ¬ҪвЦ®јҙҝЙөГіцҪбВЫЈ®
Ј¬·ЦЎПABR=90ЎгЎўЎПARB=90ЎгәНЎПBAR=90ЎгИэЦЦЗйҝцҝјВЗЈ¬АыУГ№ҙ№Й¶ЁАнјҙҝЙөГіц№ШУЪnөДТ»ФӘТ»ҙОЈЁ»тТ»ФӘ¶юҙОЈ©·ҪіМЈ¬ҪвЦ®јҙҝЙөГіцҪбВЫЈ®
ПкҪвЈәЈЁ1Ј©ЎЯPQЎНBCЈ¬MNЎНBCЈ¬ADЎНBCЈ¬ЎаPQЎОADЈ¬MNЎОADЈ¬ЎаЎчBPQЎЧЎчBADЈ¬ЎчCADЎЧЎчCMNЈ¬ЎаBQ=![]() BDЈ¬CN=
BDЈ¬CN=![]() CDЈ®
CDЈ®
ЙиPQ=xЈ¬ФтQN=BC©ҒBQ©ҒCN=120©Ғ![]() ЈЁBD+CDЈ©=©Ғ
ЈЁBD+CDЈ©=©Ғ![]() x+120Ј¬
x+120Ј¬
Ўаy=PQQN=xЈЁ©Ғ![]() x+120Ј©=©Ғ
x+120Ј©=©Ғ![]() x2+120x=©Ғ
x2+120x=©Ғ![]() ЈЁx©Ғ40Ј©2+2400Ј¬
ЈЁx©Ғ40Ј©2+2400Ј¬
Ўаөұx=40КұЈ¬yИЎЧоҙуЦө2400Ј¬ЎаҝнОӘ40mmКұЈ¬ЖдГж»эЧоҙуЈ®ЧоҙуГж»эКЗ2400mm2Ј®
ЈЁ2Ј©ўЩТАХХМвТв»ӯіцНјРОЈ¬ИзНјЛщКҫЈ®
ЙиЕЧОпПЯөДҪвОцКҪОӘy=ax2+cЈ¬Ҫ«BЈЁ©Ғ60Ј¬0Ј©ЎўAЈЁ20Ј¬80Ј©ҙъИлy=ax2+cЈ¬![]() Ј¬ҪвөГЈә
Ј¬ҪвөГЈә Ј¬Ўа№эAЎўBЎўCИэөгөДЕЧОпПЯҪвОцКҪОӘy=©Ғ
Ј¬Ўа№эAЎўBЎўCИэөгөДЕЧОпПЯҪвОцКҪОӘy=©Ғ![]() x2+90Ј®
x2+90Ј®
ўЪјЩЙиҙжФЪЈ¬ЙиөгRөДЧшұкОӘЈЁ0Ј¬nЈ©Ј¬ФтAB=80![]() Ј¬AR=
Ј¬AR=![]() Ј¬BR=
Ј¬BR=![]() Ј®
Ј®
·ЦИэЦЦЗйҝцҝјВЗЈә
ўЩөұЎПABR=90ЎгКұЈ¬УРAR2=AB2+BR2Ј¬јҙ400+ЈЁ80©ҒnЈ©2=12800+3600+n2Ј¬ҪвөГЈәn=©Ғ60Ј¬ҙЛКұөгRөДЧшұкОӘЈЁ0Ј¬©Ғ60Ј©Ј»
ўЪөұЎПARB=90ЎгКұЈ¬УРAB2=AR2+BR2Ј¬јҙ12800=400+ЈЁ80©ҒnЈ©2+3600+n2Ј¬ХыАнөГЈәn2©Ғ80n©Ғ1200=0Ј¬ҪвөГЈәn1=![]() Ј¬n2=
Ј¬n2=![]() Ј¬ҙЛКұөгRөДЧшұкОӘЈЁ0Ј¬
Ј¬ҙЛКұөгRөДЧшұкОӘЈЁ0Ј¬![]() Ј©»тЈЁ0Ј¬
Ј©»тЈЁ0Ј¬![]() Ј©Ј»
Ј©Ј»
ўЫөұЎПBAR=90ЎгКұЈ¬УРBR2=AB2+AR2Ј¬јҙ3600+n2=12800+400+ЈЁ80©ҒnЈ©2Ј¬ҪвөГЈәn=100Ј¬ҙЛКұөгRөДЧшұкОӘЈЁ0Ј¬100Ј©Ј®
ЧЫЙПЛщКцЈәФЪҙЛЕЧОпПЯ¶ФіЖЦбЙПҙжФЪТ»өгRЈ¬К№ТФAЎўBЎўRОӘ¶ҘөгөДИэҪЗРОКЗЦұҪЗИэҪЗРОЈ¬өгRөДЧшұкОӘЈЁ0Ј¬©Ғ60Ј©»тЈЁ0Ј¬![]() Ј©»тЈЁ0Ј¬
Ј©»тЈЁ0Ј¬![]() Ј©»тЈЁ0Ј¬100Ј©Ј®
Ј©»тЈЁ0Ј¬100Ј©Ј®


 ГыРЈБ·ҝјҫнЖЪД©іеҙМҫнПөБРҙр°ё
ГыРЈБ·ҝјҫнЖЪД©іеҙМҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬өИұЯЎчA1C1C2өДЦЬіӨОӘ1Ј¬ЧчC1D1ЎНA1C2УЪD1Ј¬ФЪC1C2өДСУіӨПЯЙПИЎөгC3Ј¬К№D1C3=D1C1Ј¬Б¬ҪУD1C3Ј¬ТФC2C3ОӘұЯЧчөИұЯЎчA2C2C3Ј»ЧчC2D2ЎНA2C3УЪD2Ј¬ФЪC2C3өДСУіӨПЯЙПИЎөгC4Ј¬К№D2C4=D2C2Ј¬Б¬ҪУD2C4Ј¬ТФC3C4ОӘұЯЧчөИұЯЎчA3C3C4Ј»ЎӯЗТөгA1Ј¬A2Ј¬A3Ј¬Ўӯ¶јФЪЦұПЯC1C2Н¬ІаЈ¬ИзҙЛПВИҘЈ¬ФтЎчA1C1C2Ј¬ЎчA2C2C3Ј¬ЎчA3C3C4Ј¬ЎӯЈ¬ЎчAnCnCn+1өДЦЬіӨәНОӘ______Ј®ЈЁnЎЭ2Ј¬ЗТnОӘХыКэЈ©

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬OAЎНOBЈ¬ТэЙдПЯOCЈЁөгCФЪЎПAOBНвЈ©Ј¬ИфЎПBOCЈҪҰБЈЁ0ЎгЈјҰБЈј90ЎгЈ©Ј¬ODЖҪ·ЦЎПBOCЈ¬OEЖҪ·ЦЎПAODЈ®
ЈЁ1Ј©ИфҰБЈҪ40ЎгЈ¬ЗуЎПBOEөД¶ИКэЈ»
ЈЁ2Ј©ЗлёщҫЭЎПBOCЈҪҰБЈ¬ЗлТАМвТвІ№И«НјРОЈ¬ЗуіцЎПBOEөД¶ИКэЈЁУГә¬ҰБөДКҪЧУұнКҫЈ©Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬өгPОӘ¶ЁҪЗЎПAOBөДЖҪ·ЦПЯЙПөДТ»ёц¶ЁөгЈ¬ЗТЎПMPNУлЎПAOB»ҘІ№Ј¬ИфЎПMPNФЪИЖөгPРэЧӘөД№эіМЦРЈ¬ЖдБҪұЯ·ЦұрУлOAЎўOBПаҪ»УЪMЎўNБҪөгЈ¬ФтТФПВҪбВЫЈәЈЁ1Ј©PM=PNәгіЙБўЈ»ЈЁ2Ј©OM+ONөДЦөІ»ұдЈ»ЈЁ3Ј©ЛДұЯРОPMONөДГж»эІ»ұдЈ»ЈЁ4Ј©MNөДіӨІ»ұдЈ¬ЖдЦРХэИ·өДёцКэОӘЈЁЎЎЎЎЈ©

A. 4B. 3C. 2D. 1
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
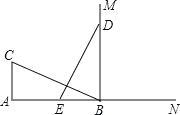
ЎҫМвДҝЎҝИзНјЈ¬CAЎНABЈ¬ҙ№ЧгОӘ AЈ¬ABЈҪ24Ј¬ACЈҪ12Ј¬ЙдПЯ BMЎНABЈ¬ҙ№ЧгОӘ BЈ¬ Т»¶Ҝөг E ҙУ Aөгіц·ўТФ 3 АеГЧ/ГлСШЙдПЯ AN ФЛ¶ҜЈ¬өг D ОӘЙдПЯ BM ЙПТ»¶ҜөгЈ¬ ЛжЧЕ E өгФЛ¶Ҝ¶шФЛ¶ҜЈ¬ЗТКјЦХұЈіЦ EDЈҪCBЈ¬өұөг E ҫӯ№э______ГлКұЈ¬ЎчDEB УлЎчBCA И«өИЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈәИзНјЈ¬ЎчABCЦРЈ¬BD=DCЈ¬ЎПABD=ЎПACDЈ¬ЗуЦӨЈәADЖҪ·ЦЎПBAC.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬AB=CBЈ¬ЎПBAC=ЎПBCAЈ¬ЎПABC=90ЎгЈ¬FОӘABСУіӨПЯЙПТ»өгЈ¬өгEФЪBCЙПЈ¬ЗТAE=CF.
(1)ЗуЦӨ:RtЎчABEЎХ RtЎчCBFЈ»
(2)ЗуЦӨ:AEЎНCFЈ»
(3)ИфЎПCAE=30ЎгЈ¬ЗуЎПACF¶ИКэ.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬Т»ҙОәҜКэ![]() өДНјПуУлЦұПЯ
өДНјПуУлЦұПЯ![]() ЖҪРРЈ¬ЗТҫӯ№эөгA(1Ј¬6).
ЖҪРРЈ¬ЗТҫӯ№эөгA(1Ј¬6).
(1)ЗуТ»ҙОәҜКэ![]() өДҪвОцКҪЈ»
өДҪвОцКҪЈ»
(2)ЗуТ»ҙОәҜКэ![]() өДНјПуУлЧшұкЦбО§іЙөДИэҪЗРОөДГж»э.
өДНјПуУлЧшұкЦбО§іЙөДИэҪЗРОөДГж»э.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ҫШРОABCDЦРЈ¬EКЗBCөДЦРөгЈ¬Б¬ҪУAEЈ¬№эөгEЧчEFЎНAEҪ»DCУЪөгFЈ¬Б¬ҪУAFЈ®Йи![]() =kЈ¬ПВБРҪбВЫЈәЈЁ1Ј©ЎчABEЎЧЎчECFЈ¬ЈЁ2Ј©AEЖҪ·ЦЎПBAFЈ¬ЈЁ3Ј©өұk=1КұЈ¬ЎчABEЎЧЎчADFЈ¬ЖдЦРҪбВЫХэИ·өДКЗЈЁЎЎЎЎЈ©
=kЈ¬ПВБРҪбВЫЈәЈЁ1Ј©ЎчABEЎЧЎчECFЈ¬ЈЁ2Ј©AEЖҪ·ЦЎПBAFЈ¬ЈЁ3Ј©өұk=1КұЈ¬ЎчABEЎЧЎчADFЈ¬ЖдЦРҪбВЫХэИ·өДКЗЈЁЎЎЎЎЈ©
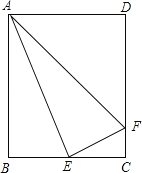
AЈ®ЈЁ1Ј©ЈЁ2Ј©ЈЁ3Ј© BЈ®ЈЁ1Ј©ЈЁ3Ј© CЈ®ЈЁ1Ј©ЈЁ2Ј© DЈ®ЈЁ2Ј©ЈЁ3Ј©
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com