
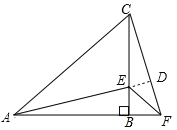
【题目】如图,在△ABC中,AB=CB,∠BAC=∠BCA,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌ Rt△CBF;
(2)求证:AE⊥CF;
(3)若∠CAE=30°,求∠ACF度数.

【答案】(1)见解析;(2)见解析;(3)∠ACF=60°
【解析】
(1)在Rt△ABE和Rt△CBF中,由于AB=CB,AE=CF,利用HL可证Rt△ABE≌Rt△CBF;
(2)延长AE交CF于D,根据三角形的内角和得∠CDE=∠ABC=90°;
(3)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠BAE的度数,又由Rt△ABE≌Rt△CBF,即可求得∠BCF的度数,则由∠ACF=∠BCF+∠ACB即可求得答案.
(1)证明:
∵∠ABC=90°
∴∠ABE=∠CBF=90°
∴△ABE和△CBF是直角三角形
∵AB=BC,AE=CF
∴Rt△ABE≌Rt△CBF(HL)
(2)延长AE交CF于D,
∵△ABE≌△CBF
∴∠BAE=∠BCF
∵∠AEB=∠CED
∴∠BAE+∠AEB=90°
∴∠DCE+∠CED=90°
∴∠CDE=90°
∴AE⊥CF.
(3)∵AB=CB,∠ABC=90°,∠CAE=30°,∠CAB=∠CAE+∠EAB,
∴∠BCA=∠BAC=45°,
∴∠EAB=15°,
∵Rt△ABE≌Rt△CBF,
∴∠EAB=∠FCB,
∴∠FCB=15°,
∴∠ACF=∠FCB+∠BCA=15°+45°=60°,
即∠ACF=60°.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象经过点A(1,3).
的图象经过点A(1,3).
(1)试确定此反比例函数的解析式;
(2)当![]() =2时, 求y的值;
=2时, 求y的值;
(3)当自变量![]() 从5增大到8时,函数值y是怎样变化的?
从5增大到8时,函数值y是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列由5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1).其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价-成本价)
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张质地、大小、背面完全相同的卡片上,正面分别画有平行四边形、矩形、等腰三角形、菱形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不低于270万元,又不超过296万元.开发建设办公室预算:一套A型“廉租房”的造价为10万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2) 在投入资金最少的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低1万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com